Choquet-Kendall-Matheron theorem

A theorem characterizing the distribution of a random closed set in terms of the Choquet capacity functional [a1]. This theorem was established independently by D.G. Kendall [a2] and G. Matheron [a3] in their work on random closed sets.

Let 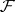and 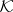be the family of closed and compact subsets of 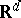, respectively. The family 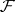is endowed with the hit-or-miss topology, which is generated by

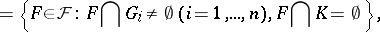for a compact set 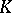and open sets 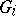. Let 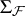be the Borel 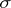-algebra generated by the hit-or-miss topology. Then 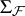is the smallest 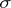-algebra of subsets of 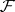containing the sets

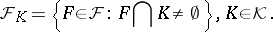Now, a random closed set 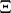is an 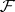-valued random element. Its distribution is described by the corresponding probability measure 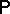on :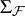

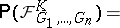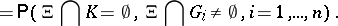This distribution can also be characterized by the functional

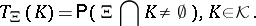The functional 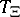is an alternating Choquet capacity of infinite order. This means that:

i) 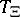is upper semi-continuous ( 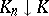implies 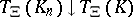; cf. also Semi-continuous function);

ii) 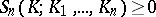, , 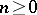where

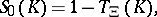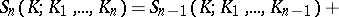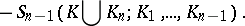The values 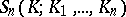can be interpreted as the probability that 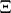does not intersect 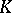but does intersect .

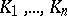The Choquet–Kendall–Matheron theorem asserts that given a functional 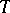on 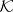, there exists a distributi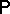on on 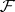with

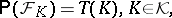if and only if 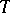is an alternating Choquet capacity of infinite order with 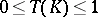and 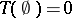. This distribution is necessarily unique.

See [a4] for applications.

References

[a1]	G. Choquet, "Theory of capacities" Ann. Inst. Fourier , V (1953-1954) pp. 131–295
[a2]	D.G. Kendall, "Foundations of a theory of random sets" E.F. Harding (ed.) D.G. Kendall (ed.) , Stochastic Geometry , Wiley (1974) pp. 322–376
[a3]	G. Matheron, "Random sets and integral geometry" , Wiley (1975)
[a4]	D. Stoyan, W.S. Kendall, J. Mecke, "Stochastic geometry and its applications" , Wiley (1995) (Edition: Second)