Difference between revisions of "Cesàro summation methods"
(Importing text file) |
Ulf Rehmann (talk | contribs) m (moved Cesàro summation methods to Cesaro summation methods: ascii title) |
(No difference)
| |
Revision as of 18:51, 24 March 2012
A collection of methods for the summation of series of numbers and functions. Introduced by E. Cesàro [1] and denoted by the symbol  .
.
A series
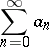 | (*) |
with partial sums  is summable by the Cesàro method of order
is summable by the Cesàro method of order  , or
, or  -summable, with sum
-summable, with sum  if
if
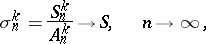 |
where 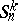 and
and 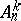 are defined as the coefficients of the expansions
are defined as the coefficients of the expansions
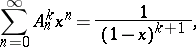 |
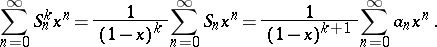 |
Expressions for 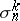 and
and 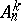 can be given in the form
can be given in the form
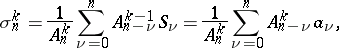 |
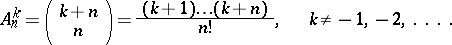 |
The method  is a matrix summation method with matrix
is a matrix summation method with matrix 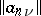 ,
,
 |
For  the method coincides with ordinary convergence, for
the method coincides with ordinary convergence, for 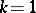 it is the method of arithmetic averages. The methods
it is the method of arithmetic averages. The methods 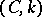 are totally regular for
are totally regular for  and are not regular for
and are not regular for 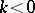 . The power of the method increases as
. The power of the method increases as  increases: If a series is summable by the method
increases: If a series is summable by the method 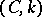 , then it is summable with the same sum by the method
, then it is summable with the same sum by the method  for
for  . This property does not hold for
. This property does not hold for  . It follows from the summability of the series (*) by the method
. It follows from the summability of the series (*) by the method 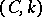 that
that  . The method
. The method 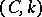 is equivalent to and compatible with the summation methods
is equivalent to and compatible with the summation methods 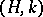 of Hölder and
of Hölder and 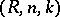 of Riesz
of Riesz  (cf. Hölder summation methods; Riesz summation method). For any
(cf. Hölder summation methods; Riesz summation method). For any  the method
the method 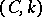 is weaker than Abel's method (cf. Abel summation method).
is weaker than Abel's method (cf. Abel summation method).
Originally, the methods 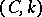 were defined by Cesàro for positive integer values of the parameter
were defined by Cesàro for positive integer values of the parameter 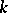 , and applied to the multiplication of series. They were later extended to arbitrary values of
, and applied to the multiplication of series. They were later extended to arbitrary values of 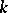 , including complex values. The methods
, including complex values. The methods  have numerous applications, e.g. to the multiplication of series, in the theory of Fourier series, and to other questions.
have numerous applications, e.g. to the multiplication of series, in the theory of Fourier series, and to other questions.
References
| [1] | E. Cesàro, Bull. Sci. Math. , 14 : 1 (1890) pp. 114–120 |
| [2] | G.H. Hardy, "Divergent series" , Clarendon Press (1949) |
| [3] | A. Zygmund, "Trigonometric series" , 1 , Cambridge Univ. Press (1988) |
| [4] | S.A. Baron, "Introduction to the theory of summability of series" , Tartu (1966) (In Russian) |
Cesàro summation methods. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Ces%C3%A0ro_summation_methods&oldid=22281