Difference between revisions of "Brooks-Jewett theorem"
(Importing text file) |
Ulf Rehmann (talk | contribs) m (moved Brooks–Jewett theorem to Brooks-Jewett theorem: ascii title) |
(No difference)
| |
Revision as of 18:51, 24 March 2012
Let 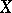 be a topological group. A set function
be a topological group. A set function 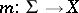 is exhaustive (also called strongly bounded) if
is exhaustive (also called strongly bounded) if  for each sequence
for each sequence 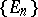 of pairwise disjoint sets from the
of pairwise disjoint sets from the  -algebra
-algebra 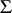 (cf. also Measure). A sequence
(cf. also Measure). A sequence 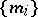 of set functions
of set functions 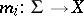 ,
, 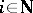 , is uniformly exhaustive if
, is uniformly exhaustive if 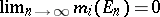 uniformly in
uniformly in 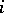 for each sequence
for each sequence 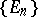 of pairwise disjoint sets from the
of pairwise disjoint sets from the 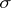 -algebra
-algebra 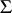 .
.
Being a generalization of the Nikodým convergence theorem, the Brooks–Jewett theorem [a1] says that for a pointwise-convergent sequence  of finitely additive scalar and exhaustive set functions (strongly additive) defined on a
of finitely additive scalar and exhaustive set functions (strongly additive) defined on a  -algebra
-algebra 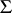 , i.e. such that
, i.e. such that 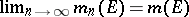 ,
, 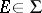 :
:
i) 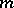 is an additive and exhaustive set function;
is an additive and exhaustive set function;
ii)  is uniformly exhaustive.
is uniformly exhaustive.
There is a generalization of the Brooks–Jewett theorem for 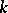 -triangular set functions defined on algebras with some weak
-triangular set functions defined on algebras with some weak 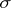 -conditions (
-conditions (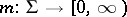 is said to be
is said to be 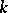 -triangular for
-triangular for 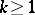 if
if 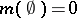 and
and
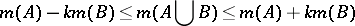 |
whenever 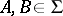 ,
, 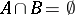 ). The following definitions are often used [a2], [a6], [a5]:
). The following definitions are often used [a2], [a6], [a5]:
SCP) An algebra 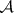 has the sequential completeness property if each disjoint sequence
has the sequential completeness property if each disjoint sequence 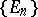 from
from 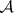 has a subsequence
has a subsequence 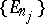 whose union is in
whose union is in 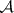 .
.
SIP) An algebra 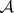 has the subsequentional interpolation property if for each subsequence
has the subsequentional interpolation property if for each subsequence 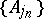 of each disjoint sequence
of each disjoint sequence 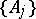 from
from 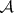 there are a subsequence
there are a subsequence 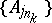 and a set
and a set 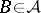 such that
such that
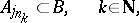 |
and 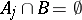 for
for 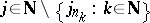 .
.
According to [a5]: Let  satisfy SIP) and let
satisfy SIP) and let 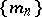 ,
, 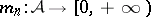 ,
, 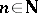 , be a sequence of
, be a sequence of 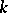 -triangular exhaustive set functions. If the limit
-triangular exhaustive set functions. If the limit
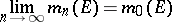 |
exists for each  and
and 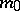 is exhaustive, then
is exhaustive, then 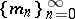 is uniformly exhaustive and
is uniformly exhaustive and 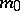 is
is 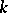 -triangular.
-triangular.
There are further generalizations of the Brooks–Jewett theorem, with respect to: the domain of the set functions (orthomodular lattices, 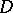 -posets); properties of the set functions; and the range (topological groups, uniform semi-groups, uniform spaces), [a2], [a4], [a5].
-posets); properties of the set functions; and the range (topological groups, uniform semi-groups, uniform spaces), [a2], [a4], [a5].
It is known that for additive set functions the Brooks–Jewett theorem is equivalent with the Nikodým convergence theorem, and even more with the Vitali–Hahn–Saks theorem [a3].
See also Diagonal theorem.
References
| [a1] | J. Brooks, R. Jewett, "On finitely additive vector measures" Proc. Nat. Acad. Sci. USA , 67 (1970) pp. 1294–1298 |
| [a2] | C. Constantinescu, "Some properties of spaces of measures" Suppl. Atti Sem. Mat. Fis. Univ. Modena , 35 (1991) pp. 1–286 |
| [a3] | L. Drewnowski, "Equivalence of Brooks–Jewett, Vitali–Hahn–Saks and Nikodým theorems" Bull. Acad. Polon. Sci. , 20 (1972) pp. 725–731 |
| [a4] | A.B. D'Andrea, P. de Lucia, "The Brooks–Jewett theorem on an orthomodular lattice" J. Math. Anal. Appl. , 154 (1991) pp. 507–522 |
| [a5] | E. Pap, "Null-additive set functions" , Kluwer Acad. Publ. &Ister Sci. (1995) |
| [a6] | H. Weber, "Compactness in spaces of group-valued contents, the Vitali–Hahn–Saks theorem and the Nikodym's boundedness theorem" Rocky Mtn. J. Math. , 16 (1986) pp. 253–275 |
Brooks-Jewett theorem. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Brooks-Jewett_theorem&oldid=22193