Briot-Bouquet equation

An ordinary differential equation

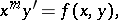(1)

where 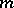is a positive integer and the function 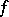is analytic at 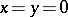, , 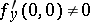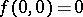. It was shown by C. Briot and T. Bouquet [1] that any equation of the type

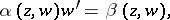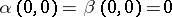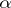where and and 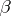are analytic at the origin, can be reduced, by means of a special local changes of the variables, to a finite number of equations of type (1). Equation (1) always (except for the case where 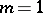and 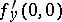is a natural number) has a unique solution in the form of a formal power series:

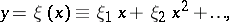(2)

which converges for sufficiently small 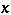if 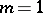, and can diverge for all 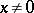if 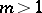. In (1), let

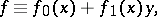then, for the series (2) to converge, it is necessary and sufficient to meet 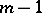conditions concerning the coefficients of the Taylor series of 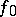and 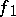; all the coefficients are included in these conditions, so that the existence or non-existence of an analytic solution 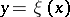of equation (1) cannot be proved by any partial sum of the Taylor series of 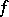(cf. [2], [3]). For the case of a general function 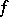there are 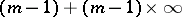such conditions, [4]. Accordingly, the Briot–Bouquet equation is sometimes referred to as equation (1) with .

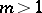References

[1]	C. Briot, T. Bouquet, "Récherches sur les proprietés des équations différentielles" J. École Polytechnique , 21 : 36 (1856) pp. 133–198
[2]	L. Bieberbach, "Theorie der gewöhnlichen Differentialgleichungen auf funktionentheoretischer Grundlage dargestellt" , Springer (1965)
[3]	A.D. Bryuno, "Analytical form of differential equations. Introduction" Trans. Moscow Math. Soc. , 25 (1971) pp. 134–151 Trudy Moskov. Mat. Obshch. , 25 (1971) pp. 120–138
[4]	J. Martinet, J.P. Ramis, "Problèmes de modules pour des équations différentielles du premier ordre" Publ. Math. IHES , 55 (1982) pp. 63–164