Difference between revisions of "Semi-invariant(2)"
(Importing text file) |
Ulf Rehmann (talk | contribs) m (MR/ZBL numbers added) |
||
| Line 18: | Line 18: | ||
====References==== | ====References==== | ||
| − | <table><TR><TD valign="top">[1]</TD> <TD valign="top"> | + | <table><TR><TD valign="top">[1]</TD> <TD valign="top"> A. Borel, "Linear algebraic groups" , Benjamin (1969) {{MR|0251042}} {{ZBL|0206.49801}} {{ZBL|0186.33201}} </TD></TR><TR><TD valign="top">[2]</TD> <TD valign="top"> J.E. Humphreys, "Linear algebraic groups" , Springer (1975) {{MR|0396773}} {{ZBL|0325.20039}} </TD></TR><TR><TD valign="top">[3]</TD> <TD valign="top"> C. Chevalley, "Théorie des groupes de Lie" , '''2''' , Hermann (1951) {{MR|0051242}} {{ZBL|0054.01303}} </TD></TR></table> |
Revision as of 14:51, 24 March 2012
A common eigenvector of a family of endomorphisms of a vector space or module. If 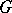 is a set of linear mappings of a vector space
is a set of linear mappings of a vector space 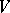 over a field
over a field 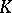 , a semi-invariant of
, a semi-invariant of 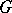 is a vector
is a vector 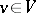 ,
, 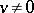 , such that
, such that
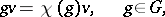 |
where 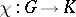 is a function, called the weight of the semi-invariant
is a function, called the weight of the semi-invariant  . A semi-invariant of weight
. A semi-invariant of weight 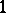 is also called an invariant. The most frequently considered case is that of a linear group
is also called an invariant. The most frequently considered case is that of a linear group 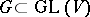 , in which case
, in which case 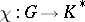 is a character of
is a character of 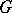 and may be extended to a polynomial function on
and may be extended to a polynomial function on 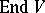 . If
. If 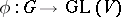 is a linear representation of a group
is a linear representation of a group 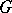 in
in 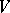 , then a semi-invariant of the group
, then a semi-invariant of the group  is also called a semi-invariant of the representation
is also called a semi-invariant of the representation 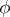 (cf. also Linear representation, invariant of a). Let
(cf. also Linear representation, invariant of a). Let 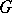 be a linear algebraic group,
be a linear algebraic group, 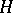 a closed subgroup of
a closed subgroup of 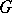 and
and 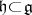 the Lie algebras of these groups. Then there exist a faithful rational linear representation
the Lie algebras of these groups. Then there exist a faithful rational linear representation  and a semi-invariant
and a semi-invariant 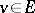 of
of 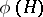 such that
such that 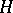 and
and 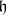 are the maximal subsets of
are the maximal subsets of 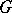 and
and 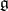 whose images in
whose images in 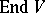 have
have  as semi-invariant. This implies that the mapping
as semi-invariant. This implies that the mapping 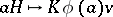 ,
, 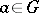 , defines an isomorphism of the algebraic homogeneous space
, defines an isomorphism of the algebraic homogeneous space 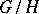 onto the orbit of the straight line
onto the orbit of the straight line 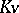 in the projective space
in the projective space 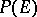 .
.
The term semi-invariant of a set 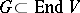 is sometimes applied to a polynomial function on
is sometimes applied to a polynomial function on 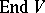 which is a semi-invariant of the set of linear mappings
which is a semi-invariant of the set of linear mappings 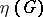 of the space
of the space 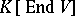 , where
, where
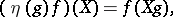 |
 |
If 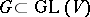 is a linear algebraic group and
is a linear algebraic group and 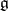 is its Lie algebra, then
is its Lie algebra, then 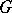 has semi-invariants
has semi-invariants
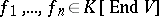 |
of the same weight such that 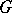 and
and  are the maximal subsets of
are the maximal subsets of 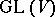 and
and  for which
for which 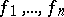 are semi-invariants (Chevalley's theorem).
are semi-invariants (Chevalley's theorem).
References
| [1] | A. Borel, "Linear algebraic groups" , Benjamin (1969) MR0251042 Zbl 0206.49801 Zbl 0186.33201 |
| [2] | J.E. Humphreys, "Linear algebraic groups" , Springer (1975) MR0396773 Zbl 0325.20039 |
| [3] | C. Chevalley, "Théorie des groupes de Lie" , 2 , Hermann (1951) MR0051242 Zbl 0054.01303 |
Semi-invariant(2). Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Semi-invariant(2)&oldid=21933