Difference between revisions of "Schubert variety"
(Importing text file) |
Ulf Rehmann (talk | contribs) m (MR/ZBL numbers added) |
||
| Line 4: | Line 4: | ||
====References==== | ====References==== | ||
| − | <table><TR><TD valign="top">[1]</TD> <TD valign="top"> | + | <table><TR><TD valign="top">[1]</TD> <TD valign="top"> H. Schubert, "Lösung des Charakteristiken-Problems für lineare Räume beliebiger Dimension" ''Mitt. Math. Gesellschaft Hamburg'' , '''1''' (1889) pp. 134–155 {{MR|}} {{ZBL|18.0631.01}} </TD></TR><TR><TD valign="top">[2]</TD> <TD valign="top"> S.L. Kleiman, "Problem 15. Rigorous foundation of Schubert's enumerative calculus" F.E. Browder (ed.) , ''Mathematical developments arising from Hilbert problems'' , ''Proc. Symp. Pure Math.'' , '''28''' , Amer. Math. Soc. (1976) pp. 445–482 {{MR|0429938}} {{ZBL|}} </TD></TR><TR><TD valign="top">[3]</TD> <TD valign="top"> P.A. Griffiths, J.E. Harris, "Principles of algebraic geometry" , '''1''' , Wiley (Interscience) (1978) {{MR|0507725}} {{ZBL|0408.14001}} </TD></TR><TR><TD valign="top">[4]</TD> <TD valign="top"> W.V.D. Hodge, D. Pedoe, "Methods of algebraic geometry" , '''2''' , Cambridge Univ. Press (1954) {{MR|0061846}} {{ZBL|0055.38705}} </TD></TR></table> |
| Line 12: | Line 12: | ||
====References==== | ====References==== | ||
| − | <table><TR><TD valign="top">[a1]</TD> <TD valign="top"> | + | <table><TR><TD valign="top">[a1]</TD> <TD valign="top"> A. Borel, "Linear algebraic groups" , Benjamin (1969) pp. 283ff {{MR|0251042}} {{ZBL|0206.49801}} {{ZBL|0186.33201}} </TD></TR><TR><TD valign="top">[a2]</TD> <TD valign="top"> M. Demazure, "Désingularisation des variétés de Schubert généralisés" ''Ann. Sci. Ecole Norm. Sup.'' , '''7''' (1974) pp. 53–87 {{MR|}} {{ZBL|}} </TD></TR><TR><TD valign="top">[a3]</TD> <TD valign="top"> V. Laksnibai, C. Seshadri, "Geometry of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s083/s083430/s08343015.png" /> - V" ''J. of Algebra'' , '''100''' (1986) pp. 462–557 {{MR|840589}} {{ZBL|}} </TD></TR></table> |
Revision as of 14:51, 24 March 2012
The set of all 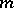 -dimensional subspaces
-dimensional subspaces 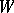 of an
of an  -dimensional vector space
-dimensional vector space  over a field
over a field  satisfying the Schubert conditions:
satisfying the Schubert conditions: 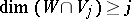 ,
, 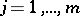 , where
, where 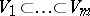 is a fixed flag of subspaces of
is a fixed flag of subspaces of 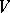 . In Grassmann coordinates these conditions are given by linear equations; a Schubert variety is an irreducible (generally speaking, singular) algebraic subvariety of the Grassmann manifold
. In Grassmann coordinates these conditions are given by linear equations; a Schubert variety is an irreducible (generally speaking, singular) algebraic subvariety of the Grassmann manifold 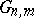 . Schubert varieties define a basis of the Chow ring
. Schubert varieties define a basis of the Chow ring 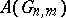 , and for
, and for 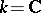 — a basis for the homology group
— a basis for the homology group 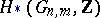 .
.
The Schubert conditions were considered by H. Schubert in connection with enumeration problems for geometric objects with given incidence properties. Hilbert's 15th problem concerns a foundation for the enumeration theory developed by Schubert (see [2]).
References
| [1] | H. Schubert, "Lösung des Charakteristiken-Problems für lineare Räume beliebiger Dimension" Mitt. Math. Gesellschaft Hamburg , 1 (1889) pp. 134–155 Zbl 18.0631.01 |
| [2] | S.L. Kleiman, "Problem 15. Rigorous foundation of Schubert's enumerative calculus" F.E. Browder (ed.) , Mathematical developments arising from Hilbert problems , Proc. Symp. Pure Math. , 28 , Amer. Math. Soc. (1976) pp. 445–482 MR0429938 |
| [3] | P.A. Griffiths, J.E. Harris, "Principles of algebraic geometry" , 1 , Wiley (Interscience) (1978) MR0507725 Zbl 0408.14001 |
| [4] | W.V.D. Hodge, D. Pedoe, "Methods of algebraic geometry" , 2 , Cambridge Univ. Press (1954) MR0061846 Zbl 0055.38705 |
Comments
The notion of a Schubert variety has been generalized to any complete homogeneous space of a semi-simple linear algebraic group 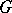 . It is the Zariski closure of any Bruhat cell ([a1]). The geometry of Schubert varieties was studied, e.g., in [a2], [a3].
. It is the Zariski closure of any Bruhat cell ([a1]). The geometry of Schubert varieties was studied, e.g., in [a2], [a3].
References
| [a1] | A. Borel, "Linear algebraic groups" , Benjamin (1969) pp. 283ff MR0251042 Zbl 0206.49801 Zbl 0186.33201 |
| [a2] | M. Demazure, "Désingularisation des variétés de Schubert généralisés" Ann. Sci. Ecole Norm. Sup. , 7 (1974) pp. 53–87 |
| [a3] | V. Laksnibai, C. Seshadri, "Geometry of 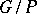 - V" J. of Algebra , 100 (1986) pp. 462–557 MR840589 - V" J. of Algebra , 100 (1986) pp. 462–557 MR840589 |
Schubert variety. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Schubert_variety&oldid=21931