Difference between revisions of "Cartan subgroup"
Ulf Rehmann (talk | contribs) m (MR/ZBL numbers added) |
Ulf Rehmann (talk | contribs) m (MR/ZBL numbers added) |
||
| Line 10: | Line 10: | ||
====References==== | ====References==== | ||
| − | <table><TR><TD valign="top">[1a]</TD> <TD valign="top"> C. Chevalley, "Theory of Lie groups" , '''1''' , Princeton Univ. Press (1946) {{MR|0082628}} {{MR|0015396}} {{ZBL|0063.00842}} </TD></TR><TR><TD valign="top">[1b]</TD> <TD valign="top"> C. Chevalley, "Théorie des groupes de Lie" , '''2–3''' , Hermann (1951–1955) {{MR|0068552}} {{MR|0051242}} {{MR|0019623}} {{ZBL|0186.33104}} {{ZBL|0054.01303}} {{ZBL|0063.00843}} </TD></TR><TR><TD valign="top">[2]</TD> <TD valign="top"> A. Borel, "Linear algebraic groups" , Benjamin (1969) {{MR|0251042}} {{ZBL|0206.49801}} {{ZBL|0186.33201}} </TD></TR><TR><TD valign="top">[3]</TD> <TD valign="top"> A. Borel, J. Tits, "Groupes réductifs" ''Publ. Math. IHES'' , '''27''' (1965) pp. 55–150 {{MR|0207712}} {{ZBL|0145.17402}} </TD></TR><TR><TD valign="top">[4]</TD> <TD valign="top"> M. Demazure, A. Grothendieck, "Schémas en groupes I-III" , ''Lect. notes in math.'' , '''151–153''' , Springer (1970) | + | <table><TR><TD valign="top">[1a]</TD> <TD valign="top"> C. Chevalley, "Theory of Lie groups" , '''1''' , Princeton Univ. Press (1946) {{MR|0082628}} {{MR|0015396}} {{ZBL|0063.00842}} </TD></TR><TR><TD valign="top">[1b]</TD> <TD valign="top"> C. Chevalley, "Théorie des groupes de Lie" , '''2–3''' , Hermann (1951–1955) {{MR|0068552}} {{MR|0051242}} {{MR|0019623}} {{ZBL|0186.33104}} {{ZBL|0054.01303}} {{ZBL|0063.00843}} </TD></TR><TR><TD valign="top">[2]</TD> <TD valign="top"> A. Borel, "Linear algebraic groups" , Benjamin (1969) {{MR|0251042}} {{ZBL|0206.49801}} {{ZBL|0186.33201}} </TD></TR><TR><TD valign="top">[3]</TD> <TD valign="top"> A. Borel, J. Tits, "Groupes réductifs" ''Publ. Math. IHES'' , '''27''' (1965) pp. 55–150 {{MR|0207712}} {{ZBL|0145.17402}} </TD></TR><TR><TD valign="top">[4]</TD> <TD valign="top"> M. Demazure, A. Grothendieck, "Schémas en groupes I-III" , ''Lect. notes in math.'' , '''151–153''' , Springer (1970) {{MR|}} {{ZBL|}} </TD></TR></table> |
Revision as of 10:19, 24 March 2012
of a group 
A maximal nilpotent subgroup  of
of  each normal subgroup of finite index of which has finite index in its normalizer in
each normal subgroup of finite index of which has finite index in its normalizer in  . If
. If  is a connected linear algebraic group over a field of characteristic zero, then a Cartan subgroup of
is a connected linear algebraic group over a field of characteristic zero, then a Cartan subgroup of  can also be defined as a closed connected subgroup whose Lie algebra is a Cartan subalgebra of the Lie algebra of
can also be defined as a closed connected subgroup whose Lie algebra is a Cartan subalgebra of the Lie algebra of  . An example of a Cartan subgroup is the subgroup
. An example of a Cartan subgroup is the subgroup  of all diagonal matrices in the group
of all diagonal matrices in the group  of all non-singular matrices.
of all non-singular matrices.
In a connected linear algebraic group  , a Cartan subgroup can also be defined as the centralizer of a maximal torus of
, a Cartan subgroup can also be defined as the centralizer of a maximal torus of 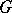 , or as a connected closed nilpotent subgroup
, or as a connected closed nilpotent subgroup 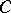 which coincides with the connected component of the identity (the identity component) of its normalizer in
which coincides with the connected component of the identity (the identity component) of its normalizer in 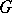 . The sets
. The sets 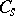 and
and 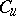 of all semi-simple and unipotent elements of
of all semi-simple and unipotent elements of 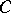 (see Jordan decomposition) are closed subgroups in
(see Jordan decomposition) are closed subgroups in 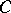 , and
, and 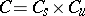 . In addition,
. In addition, 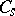 is the unique maximal torus of
is the unique maximal torus of 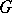 lying in
lying in  . The dimension of a Cartan subgroup of
. The dimension of a Cartan subgroup of  is called the rank of
is called the rank of  . The union of all Cartan subgroups of
. The union of all Cartan subgroups of  contains an open subset of
contains an open subset of  with respect to the Zariski topology (but is not, in general, the whole of
with respect to the Zariski topology (but is not, in general, the whole of 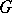 ). Every semi-simple element of
). Every semi-simple element of  lies in at least one Cartan subgroup, and every regular element in precisely one Cartan subgroup. If
lies in at least one Cartan subgroup, and every regular element in precisely one Cartan subgroup. If 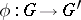 is a surjective morphism of linear algebraic groups, then the Cartan subgroups of
is a surjective morphism of linear algebraic groups, then the Cartan subgroups of  are images with respect to
are images with respect to 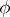 of Cartan subgroups of
of Cartan subgroups of  . Any two Cartan subgroups of
. Any two Cartan subgroups of  are conjugate. A Cartan subgroup of a connected semi-simple (or, more generally, reductive) group
are conjugate. A Cartan subgroup of a connected semi-simple (or, more generally, reductive) group  is a maximal torus in
is a maximal torus in 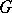 .
.
Let the group 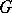 be defined over a field
be defined over a field 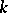 . Then there exists in
. Then there exists in  a Cartan subgroup which is also defined over
a Cartan subgroup which is also defined over 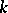 ; in fact,
; in fact,  is generated by its Cartan subgroups defined over
is generated by its Cartan subgroups defined over 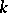 . Two Cartan subgroups of
. Two Cartan subgroups of 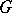 defined over
defined over 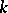 need not be conjugate over
need not be conjugate over  (but in the case when
(but in the case when  is a solvable group, they are conjugate). The variety of Cartan subgroups of
is a solvable group, they are conjugate). The variety of Cartan subgroups of 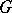 is rational over
is rational over 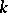 .
.
Let 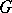 be a connected real Lie group with Lie algebra
be a connected real Lie group with Lie algebra 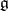 . Then the Cartan subgroups of
. Then the Cartan subgroups of 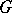 are closed in
are closed in  (but not necessarily connected) and their Lie algebras are Cartan subalgebras of
(but not necessarily connected) and their Lie algebras are Cartan subalgebras of 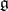 . If
. If 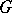 is an analytic subgroup in
is an analytic subgroup in 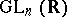 and
and  is the smallest algebraic subgroup of
is the smallest algebraic subgroup of 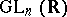 containing
containing 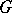 , then the Cartan subgroups of
, then the Cartan subgroups of 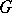 are intersections of
are intersections of 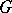 with the Cartan subgroups of
with the Cartan subgroups of 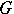 . In the case when
. In the case when 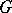 is compact, the Cartan subgroups are connected, Abelian (being maximal tori) and conjugate to one another, and every element of
is compact, the Cartan subgroups are connected, Abelian (being maximal tori) and conjugate to one another, and every element of  lies in some Cartan subgroup.
lies in some Cartan subgroup.
References
| [1a] | C. Chevalley, "Theory of Lie groups" , 1 , Princeton Univ. Press (1946) MR0082628 MR0015396 Zbl 0063.00842 |
| [1b] | C. Chevalley, "Théorie des groupes de Lie" , 2–3 , Hermann (1951–1955) MR0068552 MR0051242 MR0019623 Zbl 0186.33104 Zbl 0054.01303 Zbl 0063.00843 |
| [2] | A. Borel, "Linear algebraic groups" , Benjamin (1969) MR0251042 Zbl 0206.49801 Zbl 0186.33201 |
| [3] | A. Borel, J. Tits, "Groupes réductifs" Publ. Math. IHES , 27 (1965) pp. 55–150 MR0207712 Zbl 0145.17402 |
| [4] | M. Demazure, A. Grothendieck, "Schémas en groupes I-III" , Lect. notes in math. , 151–153 , Springer (1970) |
Comments
References
| [a1] | A. Borel, T.A. Springer, "Rationality properties of linear algebraic groups" Tohoku Math. J. (2) , 20 (1968) pp. 443–497 MR0244259 Zbl 0211.53302 |
Cartan subgroup. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Cartan_subgroup&oldid=21855