Difference between revisions of "Complexification of a Lie group"
(Importing text file) |
Ulf Rehmann (talk | contribs) m (MR/ZBL numbers added) |
||
| Line 12: | Line 12: | ||
====References==== | ====References==== | ||
| − | <table><TR><TD valign="top">[1]</TD> <TD valign="top"> M.A. Naimark, "Theory of group representations" , Springer (1982) (Translated from Russian)</TD></TR><TR><TD valign="top">[2]</TD> <TD valign="top"> D.P. Zhelobenko, "Compact Lie groups and their representations" , Amer. Math. Soc. (1973) (Translated from Russian)</TD></TR><TR><TD valign="top">[3]</TD> <TD valign="top"> N. Bourbaki, "Elements of mathematics. Lie groups and Lie algebras" , Addison-Wesley (1975) (Translated from French)</TD></TR></table> | + | <table><TR><TD valign="top">[1]</TD> <TD valign="top"> M.A. Naimark, "Theory of group representations" , Springer (1982) (Translated from Russian) {{MR|0793377}} {{ZBL|0484.22018}} </TD></TR><TR><TD valign="top">[2]</TD> <TD valign="top"> D.P. Zhelobenko, "Compact Lie groups and their representations" , Amer. Math. Soc. (1973) (Translated from Russian) {{MR|0473097}} {{MR|0473098}} {{ZBL|0228.22013}} </TD></TR><TR><TD valign="top">[3]</TD> <TD valign="top"> N. Bourbaki, "Elements of mathematics. Lie groups and Lie algebras" , Addison-Wesley (1975) (Translated from French) {{MR|0682756}} {{ZBL|0319.17002}} </TD></TR></table> |
Revision as of 10:02, 24 March 2012
over 
The complex Lie group 
containing 
as a real Lie subgroup such that the Lie algebra 
of 
is a real form of the Lie algebra 
of 
(see Complexification of a Lie algebra). One then says that the group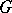 
is a real form of the Lie group 
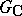. For example, the group 
of all unitary matrices of order 
is a real form of the group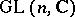 
of all non-singular matrices of order 
with complex entries.
There is a one-to-one correspondence between the complex-analytic linear representations of a connected simply-connected complex Lie group 
and the real-analytic representations of its connected real form 
, under which irreducible representations correspond to each other. This correspondence is set up in the following way: If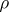 
is an (irreducible) finite-dimensional complex-analytic representation of 
, then the restriction of 
to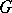 
is an (irreducible) real-analytic representation of 
.
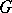Not every real Lie group has a complexification. In particular, a connected semi-simple Lie group has a complexification if and only if 
is linear, that is, is isomorphic to a subgroup of some group 
. For example, the universal covering of the group of real second-order matrices with determinant 1 does not have a complexification. On the other hand, every compact Lie group has a complexification.
The non-existence of complexifications for certain real Lie groups inspired the introduction of the more general notion of a universal complexification 
of a real Lie group 
. Here 
is a complex Lie group and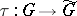 
is a real-analytic homomorphism such that for every complex Lie group 
and every real-analytic homomorphism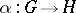 
there exists a unique complex-analytic homomorphism 
such that 
. The universal complexification of a Lie group always exists and is uniquely defined [3]. Uniqueness means that if 
is another universal complexification of 
, then there is a natural isomorphism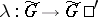 
such that 
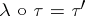. In general, 
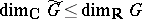, but if 
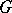is simply connected, then 
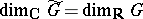and the kernel of 
is discrete.
See also Form of an algebraic group.
References
| [1] | M.A. Naimark, "Theory of group representations" , Springer (1982) (Translated from Russian) MR0793377 Zbl 0484.22018 |
| [2] | D.P. Zhelobenko, "Compact Lie groups and their representations" , Amer. Math. Soc. (1973) (Translated from Russian) MR0473097 MR0473098 Zbl 0228.22013 |
| [3] | N. Bourbaki, "Elements of mathematics. Lie groups and Lie algebras" , Addison-Wesley (1975) (Translated from French) MR0682756 Zbl 0319.17002 |
Complexification of a Lie group. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Complexification_of_a_Lie_group&oldid=21830