Borel fixed-point theorem

A connected solvable algebraic group 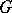acting regularly (cf. Algebraic group of transformations) on a non-empty complete algebraic variety 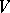over an algebraically-closed field 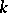has a fixed point in 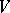. It follows from this theorem that Borel subgroups (cf. Borel subgroup) of algebraic groups are conjugate (The Borel–Morozov theorem). The theorem was demonstrated by A. Borel [1]. Borel's theorem can be generalized to an arbitrary (not necessarily algebraically-closed) field 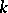: Let 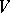be a complete variety defined over a field 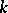on which a connected solvable 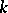-split group 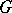acts regularly, then the set of rational 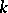-points 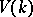is either empty or it contains a point which is fixed with respect to 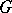. Hence the generalization of the theorem of conjugation of Borel subgroup is: If the field 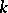is perfect, the maximal connected solvable 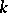-split subgroups of a connected 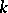-defined algebraic group 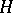are mutually conjugate by elements of the group of 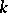-points of 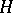[2].

References

[1]	A. Borel, "Groupes linéaires algébriques" Ann. of Math. (2) , 64 : 1 (1956) pp. 20–82 MR0093006 Zbl 0070.26104
[2]	A. Borel, "Linear algebraic groups" , Benjamin (1969) MR0251042 Zbl 0206.49801 Zbl 0186.33201
[3]	V.V. Morozov, Dokl. Akad. Nauk SSSR , 36 : 3 (1942) pp. 91–94