Difference between revisions of "Adjoint group"
Ulf Rehmann (talk | contribs) m (MR/ZBL numbers added) |
Ulf Rehmann (talk | contribs) m (MR/ZBL numbers added) |
||
| Line 4: | Line 4: | ||
====References==== | ====References==== | ||
| − | <table><TR><TD valign="top">[1]</TD> <TD valign="top"> L.S. Pontryagin, "Topological groups" , Princeton Univ. Press (1958) (Translated from Russian) | + | <table><TR><TD valign="top">[1]</TD> <TD valign="top"> L.S. Pontryagin, "Topological groups" , Princeton Univ. Press (1958) (Translated from Russian) {{MR|0201557}} {{ZBL|0022.17104}} </TD></TR><TR><TD valign="top">[2]</TD> <TD valign="top"> J.-P. Serre, "Lie algebras and Lie groups" , Benjamin (1965) (Translated from French) {{MR|0218496}} {{ZBL|0132.27803}} </TD></TR><TR><TD valign="top">[3]</TD> <TD valign="top"> J.E. Humphreys, "Linear algebraic groups" , Springer (1975) {{MR|0396773}} {{ZBL|0325.20039}} </TD></TR></table> |
Revision as of 09:19, 24 March 2012
of a group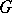 
The linear group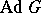 
that is the image of the Lie group or algebraic group 
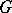under the adjoint representation (cf. Adjoint representation of a Lie group). The adjoint group 
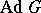is contained in the group 
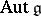of automorphisms of the Lie algebra 
of 
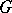, and its Lie algebra coincides with the adjoint algebra 
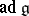of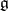 
. A connected semi-simple group is a group of adjoint type (i.e. is isomorphic to its adjoint group) if and only if its roots generate the lattice of rational characters of the maximal torus; the centre of such a group is trivial. If the ground field has characteristic zero and 
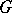is connected, then 
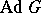is uniquely determined by the Lie algebra 
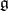and is either called the adjoint group or the group of inner automorphisms of 
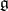. In particular, if 
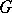is semi-simple, 
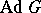coincides with the connected component of the identity in 
.
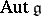References
| [1] | L.S. Pontryagin, "Topological groups" , Princeton Univ. Press (1958) (Translated from Russian) MR0201557 Zbl 0022.17104 |
| [2] | J.-P. Serre, "Lie algebras and Lie groups" , Benjamin (1965) (Translated from French) MR0218496 Zbl 0132.27803 |
| [3] | J.E. Humphreys, "Linear algebraic groups" , Springer (1975) MR0396773 Zbl 0325.20039 |
Comments
References
| [a1] | N. Bourbaki, "Elements of mathematics. Lie groups and Lie algebras" , Addison-Wesley (1975) pp. Chapt. 2; 3 (Translated from French) MR0682756 Zbl 0319.17002 |
Adjoint group. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Adjoint_group&oldid=21800