Difference between revisions of "Sample space"
From Encyclopedia of Mathematics
m (moved Sampling space to Sample space: Correcting the wrong translation from Russian) |
(terminology, and technical error) |
||
| Line 1: | Line 1: | ||
| − | The set of all [[Elementary events|elementary events]] related to some experiment, where any non-decomposable experimental result is represented by one and only one point of the | + | The set of all [[Elementary events|elementary events]] related to some experiment, where any non-decomposable experimental result is represented by one and only one point of the sample space (a sample point). The sample space is an abstract set, with a probability measure defined on the <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s083/s083220/s0832201.png" />-algebra of its subsets (cf. [[Probability space|Probability space]]). The term "space of elementary events" is frequently used in the Russian literature. |
Revision as of 17:29, 8 February 2012
The set of all elementary events related to some experiment, where any non-decomposable experimental result is represented by one and only one point of the sample space (a sample point). The sample space is an abstract set, with a probability measure defined on the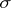 
-algebra of its subsets (cf. Probability space). The term "space of elementary events" is frequently used in the Russian literature.
Comments
References
| [a1] | W. Feller, "An introduction to probability theory and its applications" , 1 , Wiley (1957) pp. Chapt. 1 |
How to Cite This Entry:
Sample space. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Sample_space&oldid=20907
Sample space. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Sample_space&oldid=20907
This article was adapted from an original article by A.V. Prokhorov (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098. See original article