Namespaces
Variants
Actions

Difference between revisions of "Linear function"

From Encyclopedia of Mathematics
Jump to: navigation, search
m
m (Reverted edits by Rehmann (talk) to last revision by 127.0.0.1)
Line 1: Line 1:
−
A function of the form $y=kx+b$. The main property of a linear function is:
+
A function of the form <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/l/l059/l059230/l0592301.png" />. The main property of a linear function is: The increment of the function is proportional to the increment of the argument. Graphically a linear function is represented by a straight line.
−
The increment of the function is proportional to the increment of the
 
−
argument. Graphically a linear function is represented by a straight
 
−
line.
 
  
−
A linear function in $n$ variables $x_1,\dots,x_n$ is a function of the form
+
A linear function in <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/l/l059/l059230/l0592302.png" /> variables <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/l/l059/l059230/l0592303.png" /> is a function of the form
−
$$f(x) = a_1x_1+\cdots + a_nx_n +a,$$
 
−
where $a_1,\dots,a_n$ and $a$ are certain fixed numbers. The domain of definition
 
−
of a linear function is the whole $n$-dimensional space of the
 
−
variables $x_1,\dots,x_n$, real or complex. If $a=0$, the linear function is called
 
−
a homogeneous, or linear, form.
 
  
−
If all variables $x_1,\dots,x_n$ and coefficients $a_1,\dots,a_n, a$ are real (complex) numbers,
+
<table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/l/l059/l059230/l0592304.png" /></td> </tr></table>
−
then the graph of the linear function in the $n+1$-dimensional (complex)
 
−
space of the variables $x_1,\dots,x_n,y$ is the (complex) $n$-dimensional hyperplane
 
−
$y = a_1x_1+\cdots + a_nx_n +a,$, in particular, for $n=1$ it is a straight line in the plane
 
−
(respectively, a complex plane in two-dimensional complex space).
 
  
−
The term "linear function" , or, more precisely, homogeneous linear
+
where <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/l/l059/l059230/l0592305.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/l/l059/l059230/l0592306.png" /> are certain fixed numbers. The domain of definition of a linear function is the whole <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/l/l059/l059230/l0592307.png" />-dimensional space of the variables <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/l/l059/l059230/l0592308.png" />, real or complex. If <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/l/l059/l059230/l0592309.png" />, the linear function is called a homogeneous, or linear, form.
−
function, is often used for a linear mapping of a vector space $X$
+
 
−
over a field $K$ into this field, that is, for a mapping $f:X\to K$ such that
+
If all variables <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/l/l059/l059230/l05923010.png" /> and coefficients <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/l/l059/l059230/l05923011.png" /> are real (complex) numbers, then the graph of the linear function in the <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/l/l059/l059230/l05923012.png" />-dimensional (complex) space of the variables <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/l/l059/l059230/l05923013.png" /> is the (complex) <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/l/l059/l059230/l05923014.png" />-dimensional hyperplane <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/l/l059/l059230/l05923015.png" />, in particular, for <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/l/l059/l059230/l05923016.png" /> it is a straight line in the plane (respectively, a complex plane in two-dimensional complex space).
−
for any elements $x',x''\in X$ and any $\alpha',\alpha''\in K$,  
+
 
−
$$f(\alpha'x'+\alpha''x'') = \alpha'f(x') + \alpha''f(x''),$$
+
The term "linear function" , or, more precisely, homogeneous linear function, is often used for a linear mapping of a vector space <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/l/l059/l059230/l05923017.png" /> over a field <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/l/l059/l059230/l05923018.png" /> into this field, that is, for a mapping <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/l/l059/l059230/l05923019.png" /> such that for any elements <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/l/l059/l059230/l05923020.png" /> and any <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/l/l059/l059230/l05923021.png" />,
−
and in this case instead of
+
 
−
the term "linear function" one also uses the terms linear functional
+
<table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/l/l059/l059230/l05923022.png" /></td> </tr></table>
−
and linear form.
+
 
 +
and in this case instead of the term "linear function" one also uses the terms linear functional and linear form.

Revision as of 21:21, 6 December 2011

A function of the form . The main property of a linear function is: The increment of the function is proportional to the increment of the argument. Graphically a linear function is represented by a straight line.

A linear function in variables is a function of the form

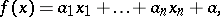where and are certain fixed numbers. The domain of definition of a linear function is the whole -dimensional space of the variables , real or complex. If , the linear function is called a homogeneous, or linear, form.

If all variables and coefficients 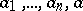are real (complex) numbers, then the graph of the linear function in the 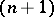-dimensional (complex) space of the variables 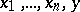is the (complex) -dimensional hyperplane , in particular, for it is a straight line in the plane (respectively, a complex plane in two-dimensional complex space).

The term "linear function" , or, more precisely, homogeneous linear function, is often used for a linear mapping of a vector space 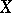over a field 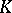into this field, that is, for a mapping 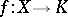such that for any elements and any ,

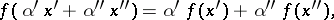and in this case instead of the term "linear function" one also uses the terms linear functional and linear form.

How to Cite This Entry:
Linear function. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Linear_function&oldid=19728
This article was adapted from an original article by L.D. Kudryavtsev (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098. See original article
Retrieved from "https://encyclopediaofmath.org/index.php?title=Linear_function&oldid=19728"