Difference between revisions of "Complex number"
(Importing text file) |
Ulf Rehmann (talk | contribs) m |
||
| Line 1: | Line 1: | ||
| − | A number of the form | + | A number of the form $z=x+iy$, where $x$ and $y$ are real numbers (cf. |
| + | [[Real number|Real number]]) and $i=\def\i{\sqrt{-1}}\i$ is the so-called imaginary unit, | ||
| + | that is, a number whose square is equal to $-1$ (in engineering | ||
| + | literature, the notation $j=\i$ is also used): $x$ is called the real | ||
| + | part of the complex number $z$ and $ y$ its imaginary part (written | ||
| + | $x=\def\Re{\mathrm{Re}\;}\Re z$, $y=\def\Im{\mathrm{Im}\;}\Im z$). The real numbers can be regarded as special complex | ||
| + | numbers, namely those with $y=0$. Complex numbers that are not real, | ||
| + | that is, for which $y\ne 0$, are sometimes called imaginary numbers. The | ||
| + | complicated historical process of the development of the notion of a | ||
| + | complex number is reflected in the above terminology which is mainly | ||
| + | of traditional origin. | ||
| − | Algebraically speaking, a complex number is an element of the (algebraic) extension | + | Algebraically speaking, a complex number is an element of the |
| + | (algebraic) extension $\C$ of the field of real numbers $\R$ obtained by | ||
| + | the adjunction to the field $\R$ of a root $i$ of the polynomial | ||
| + | $X^2+1$. The field $\C$ obtained in this way is called the field of complex | ||
| + | numbers or the complex number field. The most important property of | ||
| + | the field $\C$ is that it is algebraically closed, that is, any | ||
| + | polynomial with coefficients in $\C$ splits into linear factors. The | ||
| + | property of being algebraically closed can be expressed in other words | ||
| + | by saying that any polynomial of degree $n\ge 1$ with coefficients in $\C$ | ||
| + | has at least one root in $\C$ (the d'Alembert–Gauss theorem or | ||
| + | fundamental theorem of algebra). | ||
| − | The field | + | The field $\C$ can be constructed as follows. The elements $z=(x,y)$, $z'=(x',y'),\dots$ or |
| + | complex numbers, are taken to be the points $z=(x,y)$, $z'=(x',y'),\dots$ of the plane $\R^2$ | ||
| + | in Cartesian rectangular coordinates $x$ and $y$, $x'$ and $y',\dots$. Here | ||
| + | the sum of two complex numbers $z=(x,y)$ and $z'=(x',y')$ is the complex number $(x+x',y+y')$, | ||
| + | that is, | ||
| + | $$z+z'=(x,y)+(x',y')=(x+x',y+y'),\label{1}$$ | ||
| + | and the product of those complex numbers is the complex | ||
| + | number $(xx'-yy',xy'+x'y)$, that is, | ||
| + | $$zz'=(x,y)(x'y') = (xx'-yy',xy'+x'y).\label{2}$$ | ||
| + | The zero element $0=(0,0)$ is the same as the | ||
| + | origin of coordinates, and the complex number $(1,0)$ is the identity of | ||
| + | $\C$. | ||
| − | + | The plane $\R^2$ whose points are identified with the elements of $\C$ is | |
| + | called the complex plane. The real numbers $x,x',\dots$ are identified here | ||
| + | with the points $(x,0)$, $(x',0),\dots$ of the $x$-axis which, when referring to the | ||
| + | complex plane, is called the real axis. The points $(0,y)=iy$, $(0,y')=iy',\dots$ are | ||
| + | situated on the $y$-axis, called the imaginary axis of the complex | ||
| + | plane $\C$; numbers of the form $iy,iy',\dots$ are called pure imaginary. The | ||
| + | representation of elements $z,z',\dots$ of $\C$, or complex numbers, as points | ||
| + | of the complex plane with the rules (1) and (2) is equivalent to the | ||
| + | above more widely used form of notating complex numbers: | ||
| + | $$z=(x,y)=x+iy, z'=(x',y')=x'+iy',\dots,$$ | ||
| + | also | ||
| + | called the algebraic or Cartesian form of writing complex | ||
| + | numbers. With reference to the algebraic form, the rules (1) and (2) | ||
| + | reduce to the simple condition that all operations with complex | ||
| + | numbers are carried out as for polynomials, taking into account the | ||
| + | property of the imaginary unit: $ii=i^2=-1$. | ||
| − | and the product of | + | The complex numbers $z=(x,y)=x+iy$ and $\bar z=(x,-y)=x-iy$ are called conjugate or complex |
| + | conjugates in the plane $\C$; they are symmetrically situated with | ||
| + | respect to the real axis. The sum and the product of two conjugate | ||
| + | complex numbers are the real numbers | ||
| + | $$z+\bar z = 2\Re z,\quad z\bar z=|z|^2,$$ | ||
| + | where $|z|=r=\sqrt{x^2+y^2}$ is called the | ||
| + | modulus or absolute value of $z$. | ||
| − | + | The following inequalities always hold: | |
| + | $$|z|-|z'| \le |z+z'|\le |z|+|z'|.$$ | ||
| + | A complex number $z$ is | ||
| + | different from 0 if and only if $|z|>0$. The mapping $z\mapsto \bar z$ is an | ||
| + | automorphism of the complex plane of order 2 (that is, $z = \bar{\bar z}$) that | ||
| + | leaves all points of the real axis fixed. Furthermore, $\overline{z+z'} = \bar z + \bar{z'}$, $\bar{zz'} = \bar{z}\bar{z'}$. | ||
| − | The | + | The operations of addition and multiplication (1) and (2) are |
| + | commutative and associative, they are related by the distributive law, | ||
| + | and they have the inverse operations subtraction and division (except | ||
| + | for division by zero). The latter are expressed in algebraic form as: | ||
| − | + | $$z-z'=(x+iy)-(x'+iy')=(x-x')+i(y-y'),$$ | |
| − | + | $$\frac{z'}{z} = \frac{x'+iy'}{x+iy} = \frac{z\bar z}{|z|^2} | |
| + | =\frac{xx'+yy'}{x^2+y^2}+i\frac{y'x-x'y}{x^2+y^2},\quad z\ne0.\label{3}$$ | ||
| + | Division of a complex number $z'$ by a complex number $z\ne0$ thus | ||
| + | reduces to multiplication of $z'$ by | ||
| + | $$\frac{\bar z}{|z|^2} = \frac{x}{x^2+y^2}-i\frac{y}{x^2+y^2}.$$ | ||
| + | It is an important question | ||
| + | whether the extension $\C$ of the field of reals constructed above, | ||
| + | with the rules of operation indicated, is the only possible one or | ||
| + | whether essentially different variants are conceivable. The answer is | ||
| + | given by the uniqueness theorem: Every (algebraic) extension of the | ||
| + | field $\R$ obtained from $\R$ by adjoining a root $i$ of the equation | ||
| + | $X^2+1$ is isomorphic to $\C$, that is, only the above rules of operation | ||
| + | with complex numbers are compatible with the requirement that the root | ||
| + | $i$ be algebraically adjoined. This fact, however, does not exclude | ||
| + | the existence of interpretations of complex numbers other than as | ||
| + | points of the complex plane. The following two interpretations are | ||
| + | most frequently employed in applications. | ||
| − | + | Vector interpretation. A complex number $z=x+iy$ can be identified with the | |
| + | vector $(x,y)$ with coordinates $x$ and $y$ starting from the origin (see | ||
| + | Fig.). | ||
| − | + | <img style="border:1px solid;" | |
| − | + | src="https://www.encyclopediaofmath.org/legacyimages/common_img/c024140a.gif" /> | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | <img style="border:1px solid;" src="https://www.encyclopediaofmath.org/legacyimages/common_img/c024140a.gif" /> | ||
Figure: c024140a | Figure: c024140a | ||
| − | In this interpretation, addition and subtraction of complex numbers is carried out according to the rules of addition and subtraction of vectors. However, multiplication and division of complex numbers, which must be performed according to (2) and (3), do not have immediate analogues in vector algebra (see [[#References|[4]]], [[#References|[5]]]). The vector interpretation of complex numbers is immediately applicable, for example, in electrical engineering in the description of alternating sinusoidal currents and voltages. | + | In this interpretation, addition and subtraction of complex numbers is |
| − | + | carried out according to the rules of addition and subtraction of | |
| − | + | vectors. However, multiplication and division of complex numbers, | |
| − | + | which must be performed according to (2) and (3), do not have | |
| − | + | immediate analogues in vector algebra (see | |
| − | + | [[#References|[4]]], | |
| − | + | [[#References|[5]]]). The vector interpretation of complex numbers is | |
| − | + | immediately applicable, for example, in electrical engineering in the | |
| − | + | description of alternating sinusoidal currents and voltages. | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | Matrix interpretation. The complex number $w=u+iv$ can be identified with a | |
| + | $(2\times 2)$-matrix of special type | ||
| + | $$w=\begin{pmatrix}\phantom{-}u&v\\ -v&u\end{pmatrix}$$ | ||
| + | where the operations of addition, | ||
| + | subtraction and multiplication are carried out according to the usual | ||
| + | rules of matrix algebra. | ||
| − | + | By using polar coordinates in the complex plane $\C$, that is, the | |
| + | radius vector $r=|z|$ and polar angle $\def\phi{\varphi}\phi=\arg z$, called here the argument of $z$ | ||
| + | (sometimes also called the phase of $z$), one obtains the | ||
| + | trigonometric or polar form of a complex number: | ||
| + | $$z=r(\cos\phi + i\sin\phi),\label{4}$$ | ||
| − | + | $$r\cos\phi = \Re z,\quad r\sin\phi=\Im z.$$ | |
| + | The argument $\phi=\arg z$ is a many-valued real-valued function of the | ||
| + | complex number $z\ne 0z\ne 0$, whose values for a given $z$ differ by integral | ||
| + | multiples of $2\pi i$; the argument of the complex number $z=0$ is not | ||
| + | defined. One usually takes the principal value of the argument $\phi = \def\Arg{\mathrm{Arg}} \Arg z$, | ||
| + | defined by the additional condition $-\pi < \Arg z \le pi$. The | ||
| + | [[Euler formulas|Euler formulas]] $e^{\pm i\phi} = \cos\phi\pm i\sin\phi$ transform the trigonometric form | ||
| + | (4) into the exponential form of a complex number: | ||
| + | $$z=re^{i\phi}\label{5}$$ | ||
| + | The forms (4) | ||
| + | and (5) are particularly suitable for carrying out multiplication and | ||
| + | division of complex numbers: | ||
| + | $$zz'=rr'[\cos(\phi+\phi')+i\sin(\phi+\phi')]=rr'e^{i(\phi+\phi')},$$ | ||
| − | + | $$\frac{z}{z'}=\frac{r}{r'}[\cos(\phi-\phi')+i\sin(\phi-\phi')] | |
| + | =\frac{r}{r'}e^{i(\phi-\phi')},\quad r>0$$ | ||
| + | Under multiplication (or division) of complex numbers the moduli | ||
| + | are multiplied (or divided) and the arguments are added (or | ||
| + | subtracted). Raising to a power or extracting a root is carried out | ||
| + | according to the so-called de Moivre formulas: | ||
| + | $$z^n = r^n(\cos n\phi + i\sin n\phi) = r^n e^{in\phi},$$ | ||
| − | + | $$z^{1/n} = r^{1/n}\Big(\cos\frac{\phi+2k\pi}{n}+i\sin\frac{\phi+2k\pi}{n}\Big) | |
| + | =r^{1/n}e^{i(\phi+2k\pi)/n},$$ | ||
| − | in which the multiplicand is treated as a matrix-vector and the multiplier as a matrix-operator. | + | $$k=0,\dots,n-1,$$ |
| + | where the first of these is also applicable for negative integer | ||
| + | exponents $n$. Geometrically, multiplication of a complex number $z$ | ||
| + | by a complex number $z'=r'e^{i\phi'}$ reduces to rotating the vector $z$ over the | ||
| + | angle $\phi'$ (anti-clockwise if $\phi'>0$) and subsequently multiplying its | ||
| + | length by $|z'|=r'$; in particular, multiplication by a complex number $z'=e^{i\phi'}$, | ||
| + | which has modulus one, is merely rotation over the angle $\phi'$. Thus, | ||
| + | complex numbers can be interpreted as operators of a special type | ||
| + | (affinors, cf. | ||
| + | [[Affinor|Affinor]]). In this connection, the mixed vector-matrix | ||
| + | interpretation of multiplication of complex numbers is sometimes | ||
| + | useful: | ||
| + | $$(x,y)\begin{pmatrix}\phantom{-}u&v\\ -v&u\end{pmatrix}=(xu-yv,xv+yu),$$ | ||
| + | in which the multiplicand is treated as a matrix-vector | ||
| + | and the multiplier as a matrix-operator. | ||
| − | The bijection | + | The bijection $(x,y)\mapsto x+iy$ induces on the field $\C$ the topology of the |
| + | $2$-dimensional real vector space $\R^2$; this topology is compatible | ||
| + | with the field structure of $\C$ and thus $\C$ is a topological | ||
| + | field. The modulus $|z|$ is the Euclidean norm of the complex number | ||
| + | $z={x,y}$, and $\C$ endowed with this norm is a complex one-dimensional | ||
| + | Euclidean space, also called the complex $z$-plane. The topological | ||
| + | product $\C^n=\C\times\cdots\times\C$ ($n$ times, $n\ge 1$) is a complex $n$-dimensional Euclidean | ||
| + | space. For a satisfactory analysis of functions it is usually | ||
| + | necessary to consider their behaviour in the complex domain. This is | ||
| + | due to the fact that $\C$ is algebraically closed. Even the behaviour | ||
| + | of such elementary functions as $z^n$, $\cos z$, $\sin z$, $e^z$ can be properly | ||
| + | understood only when they are regarded as functions of a complex | ||
| + | variable (see | ||
| + | [[Analytic function|Analytic function]]). | ||
| − | Apparently, imaginary quantities first occurred in the celebrated work The great art, or the rules of algebra by G. Cardano, 1545, who regarded them as useless and unsuitable for applications. R. Bombelli (1572) was the first to realize the value of the use of imaginary quantities, in particular for the solution of the [[Cubic equation|cubic equation]] in the so-called irreducible case (when the real roots are expressed in terms of cube roots of imaginary quantities, cf. [[Cardano formula|Cardano formula]]). He gave some of the simplest rules of operation with complex numbers. In general, expressions of the form | + | Apparently, imaginary quantities first occurred in the celebrated work |
| + | The great art, or the rules of algebra by G. Cardano, 1545, who | ||
| + | regarded them as useless and unsuitable for applications. R. Bombelli | ||
| + | (1572) was the first to realize the value of the use of imaginary | ||
| + | quantities, in particular for the solution of the | ||
| + | [[Cubic equation|cubic equation]] in the so-called irreducible case | ||
| + | (when the real roots are expressed in terms of cube roots of imaginary | ||
| + | quantities, cf. | ||
| + | [[Cardano formula|Cardano formula]]). He gave some of the simplest | ||
| + | rules of operation with complex numbers. In general, expressions of | ||
| + | the form $a+b\i$, $b\ne 0$, appearing in the solution of quadratic and cubic | ||
| + | equations were called "imaginary" in the 16th century and 17th | ||
| + | century. However, even for many of the great scholars of the 17th | ||
| + | century, the algebraic and geometric nature of imaginary quantities | ||
| + | was unclear and even mystical. It is known, for example, that | ||
| + | I. Newton did not include imaginary quantities within the notion of | ||
| + | number, and that G. Leibniz said that "complex numbers are a fine and | ||
| + | wonderful refuge of the divine spirit, as if it were an amphibian of | ||
| + | existence and non-existence" . | ||
| − | The problem of expressing the | + | The problem of expressing the $n$-th roots of a given number was |
| + | mainly solved in the papers of A. de Moivre (1707, 1724) and R. Cotes | ||
| + | (1722). The symbol $i=\i$ was proposed by L. Euler (1777, published | ||
| + | 1794). It was he who in 1751 asserted that the field $\C$ is | ||
| + | algebraically closed; J. d'Alembert (1747) came to the same | ||
| + | conclusion. The first rigorous proof of this fact is due to C.F. Gauss | ||
| + | (1799), who introduced the term "complex number" in 1831. The complete | ||
| + | geometric interpretation of complex numbers and operations on them | ||
| + | appeared first in the work of C. Wessel (1799). The geometric | ||
| + | representation of complex numbers, sometimes called the "Argand | ||
| + | diagramArgand diagram" , came into use after the publication in 1806 | ||
| + | and 1814 of papers by J.R. Argand, who rediscovered, largely | ||
| + | independently, the findings of Wessel. | ||
| − | The purely arithmetic theory of complex numbers as pairs of real numbers was introduced by W. Hamilton (1837). He found a generalization of complex numbers, namely the quaternions (cf. [[Quaternion|Quaternion]]), which form a non-commutative algebra. More generally, it was proved at the end of the 19th century that any extension of the notion of number beyond the complex numbers requires sacrificing some property of the usual operations (primarily commutativity). See also [[Hypercomplex number|Hypercomplex number]]; [[Double and dual numbers|Double and dual numbers]]; [[Cayley numbers|Cayley numbers]]. | + | The purely arithmetic theory of complex numbers as pairs of real |
| + | numbers was introduced by W. Hamilton (1837). He found a | ||
| + | generalization of complex numbers, namely the quaternions (cf. | ||
| + | [[Quaternion|Quaternion]]), which form a non-commutative algebra. More | ||
| + | generally, it was proved at the end of the 19th century that any | ||
| + | extension of the notion of number beyond the complex numbers requires | ||
| + | sacrificing some property of the usual operations (primarily | ||
| + | commutativity). See also | ||
| + | [[Hypercomplex number|Hypercomplex number]]; | ||
| + | [[Double and dual numbers|Double and dual numbers]]; | ||
| + | [[Cayley numbers|Cayley numbers]]. | ||
====References==== | ====References==== | ||
| − | <table><TR><TD valign="top">[1]</TD> <TD valign="top"> | + | <table><TR><TD valign="top">[1]</TD> |
| + | <TD valign="top"> A.G. Kurosh, "Higher algebra" , MIR (1972) (Translated from Russian)</TD> | ||
| + | </TR><TR><TD valign="top">[2]</TD> | ||
| + | <TD valign="top"> A.I. Kostrikin, "Introduction to algebra" , Springer (1982) (Translated from Russian)</TD> | ||
| + | </TR><TR><TD valign="top">[3]</TD> | ||
| + | <TD valign="top"> A.I. Markushevich, "Theory of functions of a complex variable" , '''1–2''' , Chelsea (1977) (Translated from Russian)</TD> | ||
| + | </TR><TR><TD valign="top">[4]</TD> | ||
| + | <TD valign="top"> B.V. Shabat, "Introduction of complex analysis" , '''1''' , Moscow (1976) (In Russian)</TD> | ||
| + | </TR><TR><TD valign="top">[5]</TD> | ||
| + | <TD valign="top"> M.A. [M.A. Lavrent'ev] Lawrentjew, B.V. [B.V. Shabat] Schabat, "Problems in hydrodynamics and their mathematical models" , Moscow (1973) (In Russian)</TD> | ||
| + | </TR><TR><TD valign="top">[6]</TD> | ||
| + | <TD valign="top"> A. Hurwitz, R. Courant, "Vorlesungen über allgemeine Funktionentheorie und elliptische Funktionen" , Springer (1968)</TD> | ||
| + | </TR><TR><TD valign="top">[7]</TD> | ||
| + | <TD valign="top"> G.H. Hardy, "A course of pure mathematics" , Cambridge Univ. Press (1955)</TD> | ||
| + | </TR><TR><TD valign="top">[8]</TD> | ||
| + | <TD valign="top"> N. Bourbaki, "Elements of mathematics. General topology" , Addison-Wesley (1966) (Translated from French)</TD> | ||
| + | </TR></table> | ||
Revision as of 21:57, 22 November 2011
A number of the form $z=x+iy$, where $x$ and $y$ are real numbers (cf. Real number) and $i=\def\i{\sqrt{-1}}\i$ is the so-called imaginary unit, that is, a number whose square is equal to $-1$ (in engineering literature, the notation $j=\i$ is also used): $x$ is called the real part of the complex number $z$ and $ y$ its imaginary part (written $x=\def\Re{\mathrm{Re}\;}\Re z$, $y=\def\Im{\mathrm{Im}\;}\Im z$). The real numbers can be regarded as special complex numbers, namely those with $y=0$. Complex numbers that are not real, that is, for which $y\ne 0$, are sometimes called imaginary numbers. The complicated historical process of the development of the notion of a complex number is reflected in the above terminology which is mainly of traditional origin.
Algebraically speaking, a complex number is an element of the (algebraic) extension $\C$ of the field of real numbers $\R$ obtained by the adjunction to the field $\R$ of a root $i$ of the polynomial $X^2+1$. The field $\C$ obtained in this way is called the field of complex numbers or the complex number field. The most important property of the field $\C$ is that it is algebraically closed, that is, any polynomial with coefficients in $\C$ splits into linear factors. The property of being algebraically closed can be expressed in other words by saying that any polynomial of degree $n\ge 1$ with coefficients in $\C$ has at least one root in $\C$ (the d'Alembert–Gauss theorem or fundamental theorem of algebra).
The field $\C$ can be constructed as follows. The elements $z=(x,y)$, $z'=(x',y'),\dots$ or complex numbers, are taken to be the points $z=(x,y)$, $z'=(x',y'),\dots$ of the plane $\R^2$ in Cartesian rectangular coordinates $x$ and $y$, $x'$ and $y',\dots$. Here the sum of two complex numbers $z=(x,y)$ and $z'=(x',y')$ is the complex number $(x+x',y+y')$, that is, $$z+z'=(x,y)+(x',y')=(x+x',y+y'),\label{1}$$ and the product of those complex numbers is the complex number $(xx'-yy',xy'+x'y)$, that is, $$zz'=(x,y)(x'y') = (xx'-yy',xy'+x'y).\label{2}$$ The zero element $0=(0,0)$ is the same as the origin of coordinates, and the complex number $(1,0)$ is the identity of $\C$.
The plane $\R^2$ whose points are identified with the elements of $\C$ is called the complex plane. The real numbers $x,x',\dots$ are identified here with the points $(x,0)$, $(x',0),\dots$ of the $x$-axis which, when referring to the complex plane, is called the real axis. The points $(0,y)=iy$, $(0,y')=iy',\dots$ are situated on the $y$-axis, called the imaginary axis of the complex plane $\C$; numbers of the form $iy,iy',\dots$ are called pure imaginary. The representation of elements $z,z',\dots$ of $\C$, or complex numbers, as points of the complex plane with the rules (1) and (2) is equivalent to the above more widely used form of notating complex numbers: $$z=(x,y)=x+iy, z'=(x',y')=x'+iy',\dots,$$ also called the algebraic or Cartesian form of writing complex numbers. With reference to the algebraic form, the rules (1) and (2) reduce to the simple condition that all operations with complex numbers are carried out as for polynomials, taking into account the property of the imaginary unit: $ii=i^2=-1$.
The complex numbers $z=(x,y)=x+iy$ and $\bar z=(x,-y)=x-iy$ are called conjugate or complex conjugates in the plane $\C$; they are symmetrically situated with respect to the real axis. The sum and the product of two conjugate complex numbers are the real numbers $$z+\bar z = 2\Re z,\quad z\bar z=|z|^2,$$ where $|z|=r=\sqrt{x^2+y^2}$ is called the modulus or absolute value of $z$.
The following inequalities always hold: $$|z|-|z'| \le |z+z'|\le |z|+|z'|.$$ A complex number $z$ is different from 0 if and only if $|z|>0$. The mapping $z\mapsto \bar z$ is an automorphism of the complex plane of order 2 (that is, $z = \bar{\bar z}$) that leaves all points of the real axis fixed. Furthermore, $\overline{z+z'} = \bar z + \bar{z'}$, $\bar{zz'} = \bar{z}\bar{z'}$.
The operations of addition and multiplication (1) and (2) are commutative and associative, they are related by the distributive law, and they have the inverse operations subtraction and division (except for division by zero). The latter are expressed in algebraic form as:
$$z-z'=(x+iy)-(x'+iy')=(x-x')+i(y-y'),$$
$$\frac{z'}{z} = \frac{x'+iy'}{x+iy} = \frac{z\bar z}{|z|^2} =\frac{xx'+yy'}{x^2+y^2}+i\frac{y'x-x'y}{x^2+y^2},\quad z\ne0.\label{3}$$ Division of a complex number $z'$ by a complex number $z\ne0$ thus reduces to multiplication of $z'$ by $$\frac{\bar z}{|z|^2} = \frac{x}{x^2+y^2}-i\frac{y}{x^2+y^2}.$$ It is an important question whether the extension $\C$ of the field of reals constructed above, with the rules of operation indicated, is the only possible one or whether essentially different variants are conceivable. The answer is given by the uniqueness theorem: Every (algebraic) extension of the field $\R$ obtained from $\R$ by adjoining a root $i$ of the equation $X^2+1$ is isomorphic to $\C$, that is, only the above rules of operation with complex numbers are compatible with the requirement that the root $i$ be algebraically adjoined. This fact, however, does not exclude the existence of interpretations of complex numbers other than as points of the complex plane. The following two interpretations are most frequently employed in applications.
Vector interpretation. A complex number $z=x+iy$ can be identified with the vector $(x,y)$ with coordinates $x$ and $y$ starting from the origin (see Fig.).
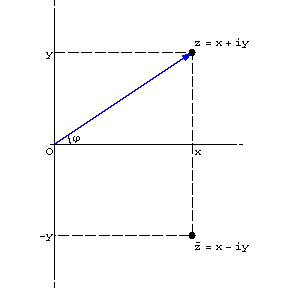
Figure: c024140a
In this interpretation, addition and subtraction of complex numbers is carried out according to the rules of addition and subtraction of vectors. However, multiplication and division of complex numbers, which must be performed according to (2) and (3), do not have immediate analogues in vector algebra (see [4], [5]). The vector interpretation of complex numbers is immediately applicable, for example, in electrical engineering in the description of alternating sinusoidal currents and voltages.
Matrix interpretation. The complex number $w=u+iv$ can be identified with a $(2\times 2)$-matrix of special type $$w=\begin{pmatrix}\phantom{-}u&v\\ -v&u\end{pmatrix}$$ where the operations of addition, subtraction and multiplication are carried out according to the usual rules of matrix algebra.
By using polar coordinates in the complex plane $\C$, that is, the radius vector $r=|z|$ and polar angle $\def\phi{\varphi}\phi=\arg z$, called here the argument of $z$ (sometimes also called the phase of $z$), one obtains the trigonometric or polar form of a complex number: $$z=r(\cos\phi + i\sin\phi),\label{4}$$
$$r\cos\phi = \Re z,\quad r\sin\phi=\Im z.$$ The argument $\phi=\arg z$ is a many-valued real-valued function of the complex number $z\ne 0z\ne 0$, whose values for a given $z$ differ by integral multiples of $2\pi i$; the argument of the complex number $z=0$ is not defined. One usually takes the principal value of the argument $\phi = \def\Arg{\mathrm{Arg}} \Arg z$, defined by the additional condition $-\pi < \Arg z \le pi$. The Euler formulas $e^{\pm i\phi} = \cos\phi\pm i\sin\phi$ transform the trigonometric form (4) into the exponential form of a complex number: $$z=re^{i\phi}\label{5}$$ The forms (4) and (5) are particularly suitable for carrying out multiplication and division of complex numbers: $$zz'=rr'[\cos(\phi+\phi')+i\sin(\phi+\phi')]=rr'e^{i(\phi+\phi')},$$
$$\frac{z}{z'}=\frac{r}{r'}[\cos(\phi-\phi')+i\sin(\phi-\phi')] =\frac{r}{r'}e^{i(\phi-\phi')},\quad r>0$$ Under multiplication (or division) of complex numbers the moduli are multiplied (or divided) and the arguments are added (or subtracted). Raising to a power or extracting a root is carried out according to the so-called de Moivre formulas: $$z^n = r^n(\cos n\phi + i\sin n\phi) = r^n e^{in\phi},$$
$$z^{1/n} = r^{1/n}\Big(\cos\frac{\phi+2k\pi}{n}+i\sin\frac{\phi+2k\pi}{n}\Big) =r^{1/n}e^{i(\phi+2k\pi)/n},$$
$$k=0,\dots,n-1,$$ where the first of these is also applicable for negative integer exponents $n$. Geometrically, multiplication of a complex number $z$ by a complex number $z'=r'e^{i\phi'}$ reduces to rotating the vector $z$ over the angle $\phi'$ (anti-clockwise if $\phi'>0$) and subsequently multiplying its length by $|z'|=r'$; in particular, multiplication by a complex number $z'=e^{i\phi'}$, which has modulus one, is merely rotation over the angle $\phi'$. Thus, complex numbers can be interpreted as operators of a special type (affinors, cf. Affinor). In this connection, the mixed vector-matrix interpretation of multiplication of complex numbers is sometimes useful: $$(x,y)\begin{pmatrix}\phantom{-}u&v\\ -v&u\end{pmatrix}=(xu-yv,xv+yu),$$ in which the multiplicand is treated as a matrix-vector and the multiplier as a matrix-operator.
The bijection $(x,y)\mapsto x+iy$ induces on the field $\C$ the topology of the $2$-dimensional real vector space $\R^2$; this topology is compatible with the field structure of $\C$ and thus $\C$ is a topological field. The modulus $|z|$ is the Euclidean norm of the complex number $z={x,y}$, and $\C$ endowed with this norm is a complex one-dimensional Euclidean space, also called the complex $z$-plane. The topological product $\C^n=\C\times\cdots\times\C$ ($n$ times, $n\ge 1$) is a complex $n$-dimensional Euclidean space. For a satisfactory analysis of functions it is usually necessary to consider their behaviour in the complex domain. This is due to the fact that $\C$ is algebraically closed. Even the behaviour of such elementary functions as $z^n$, $\cos z$, $\sin z$, $e^z$ can be properly understood only when they are regarded as functions of a complex variable (see Analytic function).
Apparently, imaginary quantities first occurred in the celebrated work The great art, or the rules of algebra by G. Cardano, 1545, who regarded them as useless and unsuitable for applications. R. Bombelli (1572) was the first to realize the value of the use of imaginary quantities, in particular for the solution of the cubic equation in the so-called irreducible case (when the real roots are expressed in terms of cube roots of imaginary quantities, cf. Cardano formula). He gave some of the simplest rules of operation with complex numbers. In general, expressions of the form $a+b\i$, $b\ne 0$, appearing in the solution of quadratic and cubic equations were called "imaginary" in the 16th century and 17th century. However, even for many of the great scholars of the 17th century, the algebraic and geometric nature of imaginary quantities was unclear and even mystical. It is known, for example, that I. Newton did not include imaginary quantities within the notion of number, and that G. Leibniz said that "complex numbers are a fine and wonderful refuge of the divine spirit, as if it were an amphibian of existence and non-existence" .
The problem of expressing the $n$-th roots of a given number was mainly solved in the papers of A. de Moivre (1707, 1724) and R. Cotes (1722). The symbol $i=\i$ was proposed by L. Euler (1777, published 1794). It was he who in 1751 asserted that the field $\C$ is algebraically closed; J. d'Alembert (1747) came to the same conclusion. The first rigorous proof of this fact is due to C.F. Gauss (1799), who introduced the term "complex number" in 1831. The complete geometric interpretation of complex numbers and operations on them appeared first in the work of C. Wessel (1799). The geometric representation of complex numbers, sometimes called the "Argand diagramArgand diagram" , came into use after the publication in 1806 and 1814 of papers by J.R. Argand, who rediscovered, largely independently, the findings of Wessel.
The purely arithmetic theory of complex numbers as pairs of real numbers was introduced by W. Hamilton (1837). He found a generalization of complex numbers, namely the quaternions (cf. Quaternion), which form a non-commutative algebra. More generally, it was proved at the end of the 19th century that any extension of the notion of number beyond the complex numbers requires sacrificing some property of the usual operations (primarily commutativity). See also Hypercomplex number; Double and dual numbers; Cayley numbers.
References
| [1] | A.G. Kurosh, "Higher algebra" , MIR (1972) (Translated from Russian) |
| [2] | A.I. Kostrikin, "Introduction to algebra" , Springer (1982) (Translated from Russian) |
| [3] | A.I. Markushevich, "Theory of functions of a complex variable" , 1–2 , Chelsea (1977) (Translated from Russian) |
| [4] | B.V. Shabat, "Introduction of complex analysis" , 1 , Moscow (1976) (In Russian) |
| [5] | M.A. [M.A. Lavrent'ev] Lawrentjew, B.V. [B.V. Shabat] Schabat, "Problems in hydrodynamics and their mathematical models" , Moscow (1973) (In Russian) |
| [6] | A. Hurwitz, R. Courant, "Vorlesungen über allgemeine Funktionentheorie und elliptische Funktionen" , Springer (1968) |
| [7] | G.H. Hardy, "A course of pure mathematics" , Cambridge Univ. Press (1955) |
| [8] | N. Bourbaki, "Elements of mathematics. General topology" , Addison-Wesley (1966) (Translated from French) |
Complex number. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Complex_number&oldid=19688