Difference between revisions of "Seidel method"
Ulf Rehmann (talk | contribs) m (tex encoded by computer) |
Ulf Rehmann (talk | contribs) m (Undo revision 48644 by Ulf Rehmann (talk)) Tag: Undo |
||
| Line 1: | Line 1: | ||
| − | < | + | An iterative method for solving a system of linear algebraic equations <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s083/s083810/s0838101.png" />. The solution <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s083/s083810/s0838102.png" /> is found as the limit of a sequence |
| − | s0838101.png | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s083/s083810/s0838103.png" /></td> </tr></table> | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
the terms of which are computed from the formula | the terms of which are computed from the formula | ||
| − | + | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s083/s083810/s0838104.png" /></td> <td valign="top" style="width:5%;text-align:right;">(*)</td></tr></table> | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s083/s083810/s0838105.png" /></td> </tr></table> | |
| − | |||
| − | |||
| − | where the | + | where the <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s083/s083810/s0838106.png" /> are the entries of the matrix <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s083/s083810/s0838107.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s083/s083810/s0838108.png" /> the components of the vector <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s083/s083810/s0838109.png" />, and the diagonal entries of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s083/s083810/s08381010.png" /> are assumed to be <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s083/s083810/s08381011.png" />. The use of (*) differs from the [[Simple-iteration method|simple-iteration method]] only in the fact that, at step <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s083/s083810/s08381012.png" />, computation of the <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s083/s083810/s08381013.png" />-th component utilizes the previously computed <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s083/s083810/s08381014.png" />-th approximations of the first <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s083/s083810/s08381015.png" /> components. |
| − | are the entries of the matrix | ||
| − | |||
| − | the components of the vector | ||
| − | and the diagonal entries of | ||
| − | are assumed to be | ||
| − | The use of (*) differs from the [[Simple-iteration method|simple-iteration method]] only in the fact that, at step | ||
| − | computation of the | ||
| − | th component utilizes the previously computed | ||
| − | th approximations of the first | ||
| − | components. | ||
| − | The Seidel method can be expressed in matrix notation as follows. If | + | The Seidel method can be expressed in matrix notation as follows. If <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s083/s083810/s08381016.png" />, where |
| − | where | ||
| − | + | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s083/s083810/s08381017.png" /></td> </tr></table> | |
| − | |||
| − | |||
| − | + | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s083/s083810/s08381018.png" /></td> </tr></table> | |
| − | |||
| − | then formula (*) in matrix notation is | + | then formula (*) in matrix notation is <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s083/s083810/s08381019.png" />. The Seidel method is equivalent to simple iteration applied to the system <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s083/s083810/s08381020.png" />, which is equivalent to the initial system. The method is convergent if and only if all the eigenvalues of the matrix <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s083/s083810/s08381021.png" /> are less than 1 in absolute value, or, equivalently, if all roots of the equation <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s083/s083810/s08381022.png" /> are less than 1 in absolute value. |
| − | The Seidel method is equivalent to simple iteration applied to the system | ||
| − | which is equivalent to the initial system. The method is convergent if and only if all the eigenvalues of the matrix | ||
| − | are less than 1 in absolute value, or, equivalently, if all roots of the equation | ||
| − | are less than 1 in absolute value. | ||
| − | In practical work, the following sufficient conditions for convergence are more convenient. 1) Suppose that | + | In practical work, the following sufficient conditions for convergence are more convenient. 1) Suppose that <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s083/s083810/s08381023.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s083/s083810/s08381024.png" />, for all <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s083/s083810/s08381025.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s083/s083810/s08381026.png" />; then the Seidel method is convergent and the following estimate holds for the rate of convergence: |
| − | |||
| − | for all | ||
| − | |||
| − | then the Seidel method is convergent and the following estimate holds for the rate of convergence: | ||
| − | + | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s083/s083810/s08381027.png" /></td> </tr></table> | |
| − | |||
| − | |||
| − | 2) If | + | 2) If <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s083/s083810/s08381028.png" /> is a positive-definite Hermitian matrix, then the Seidel method is convergent. |
| − | is a positive-definite Hermitian matrix, then the Seidel method is convergent. | ||
The method falls into the category of relaxation methods (cf. [[Relaxation method|Relaxation method]]), the most widely used of which is the [[Hyperrelaxation method|hyperrelaxation method]]. | The method falls into the category of relaxation methods (cf. [[Relaxation method|Relaxation method]]), the most widely used of which is the [[Hyperrelaxation method|hyperrelaxation method]]. | ||
| − | Among the available modifications of the Seidel method are methods that employ preliminary transformation of the system into an equivalent system | + | Among the available modifications of the Seidel method are methods that employ preliminary transformation of the system into an equivalent system <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s083/s083810/s08381029.png" /> (see [[#References|[4]]]). |
| − | see [[#References|[4]]]). | ||
The method was proposed by L. Seidel in [[#References|[1]]]. | The method was proposed by L. Seidel in [[#References|[1]]]. | ||
| Line 87: | Line 33: | ||
====References==== | ====References==== | ||
<table><TR><TD valign="top">[1]</TD> <TD valign="top"> L. Seidel, ''Abh. Bayer. Akad. Wiss. Math.-Naturwiss. Kl.'' , '''11''' : 3 (1874) pp. 81–108</TD></TR><TR><TD valign="top">[2]</TD> <TD valign="top"> N.S. Bakhvalov, "Numerical methods: analysis, algebra, ordinary differential equations" , MIR (1977) (Translated from Russian)</TD></TR><TR><TD valign="top">[3]</TD> <TD valign="top"> I.S. Berezin, N.P. Zhidkov, "Computing methods" , Pergamon (1973) (Translated from Russian)</TD></TR><TR><TD valign="top">[4]</TD> <TD valign="top"> D.K. Faddeev, V.N. Faddeeva, "Computational methods of linear algebra" , Freeman (1963) (Translated from Russian)</TD></TR></table> | <table><TR><TD valign="top">[1]</TD> <TD valign="top"> L. Seidel, ''Abh. Bayer. Akad. Wiss. Math.-Naturwiss. Kl.'' , '''11''' : 3 (1874) pp. 81–108</TD></TR><TR><TD valign="top">[2]</TD> <TD valign="top"> N.S. Bakhvalov, "Numerical methods: analysis, algebra, ordinary differential equations" , MIR (1977) (Translated from Russian)</TD></TR><TR><TD valign="top">[3]</TD> <TD valign="top"> I.S. Berezin, N.P. Zhidkov, "Computing methods" , Pergamon (1973) (Translated from Russian)</TD></TR><TR><TD valign="top">[4]</TD> <TD valign="top"> D.K. Faddeev, V.N. Faddeeva, "Computational methods of linear algebra" , Freeman (1963) (Translated from Russian)</TD></TR></table> | ||
| + | |||
| + | |||
====Comments==== | ====Comments==== | ||
Revision as of 14:53, 7 June 2020
An iterative method for solving a system of linear algebraic equations  . The solution
. The solution  is found as the limit of a sequence
is found as the limit of a sequence
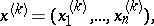 |
the terms of which are computed from the formula
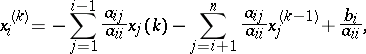 | (*) |
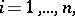 |
where the  are the entries of the matrix
are the entries of the matrix  ,
,  the components of the vector
the components of the vector  , and the diagonal entries of
, and the diagonal entries of 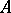 are assumed to be
are assumed to be 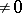 . The use of (*) differs from the simple-iteration method only in the fact that, at step
. The use of (*) differs from the simple-iteration method only in the fact that, at step 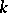 , computation of the
, computation of the  -th component utilizes the previously computed
-th component utilizes the previously computed  -th approximations of the first
-th approximations of the first 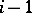 components.
components.
The Seidel method can be expressed in matrix notation as follows. If 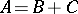 , where
, where
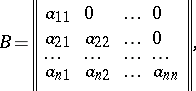 |
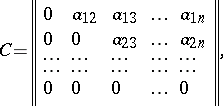 |
then formula (*) in matrix notation is 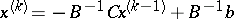 . The Seidel method is equivalent to simple iteration applied to the system
. The Seidel method is equivalent to simple iteration applied to the system 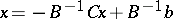 , which is equivalent to the initial system. The method is convergent if and only if all the eigenvalues of the matrix
, which is equivalent to the initial system. The method is convergent if and only if all the eigenvalues of the matrix 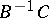 are less than 1 in absolute value, or, equivalently, if all roots of the equation
are less than 1 in absolute value, or, equivalently, if all roots of the equation 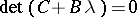 are less than 1 in absolute value.
are less than 1 in absolute value.
In practical work, the following sufficient conditions for convergence are more convenient. 1) Suppose that  ,
, 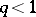 , for all
, for all 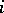 ,
, 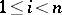 ; then the Seidel method is convergent and the following estimate holds for the rate of convergence:
; then the Seidel method is convergent and the following estimate holds for the rate of convergence:
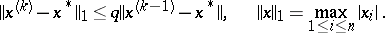 |
2) If 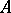 is a positive-definite Hermitian matrix, then the Seidel method is convergent.
is a positive-definite Hermitian matrix, then the Seidel method is convergent.
The method falls into the category of relaxation methods (cf. Relaxation method), the most widely used of which is the hyperrelaxation method.
Among the available modifications of the Seidel method are methods that employ preliminary transformation of the system into an equivalent system 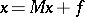 (see [4]).
(see [4]).
The method was proposed by L. Seidel in [1].
References
| [1] | L. Seidel, Abh. Bayer. Akad. Wiss. Math.-Naturwiss. Kl. , 11 : 3 (1874) pp. 81–108 |
| [2] | N.S. Bakhvalov, "Numerical methods: analysis, algebra, ordinary differential equations" , MIR (1977) (Translated from Russian) |
| [3] | I.S. Berezin, N.P. Zhidkov, "Computing methods" , Pergamon (1973) (Translated from Russian) |
| [4] | D.K. Faddeev, V.N. Faddeeva, "Computational methods of linear algebra" , Freeman (1963) (Translated from Russian) |
Comments
In the West this method is usually referred to as the Gauss–Seidel method, [a1]–[a4].
References
| [a1] | C.-E. Fröberg, "Introduction to numerical analysis" , Addison-Wesley (1965) pp. §4.5 |
| [a2] | W.H. Press, B.P. Flannery, S.A. Teukolsky, W.T. Vetterling, "Numerical recipes" , Cambridge Univ. Press (1986) pp. §17.5 |
| [a3] | D.M. Young, R.T. Gregory, "A survey of numerical mathematics" , II , Dover, reprint (1988) pp. §16.5 |
| [a4] | F.B. Hildebrand, "Introduction to numerical analysis" , Dover, reprint (1987) pp. §10.5 |
Seidel method. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Seidel_method&oldid=48644