Namespaces
Variants
Actions

Difference between revisions of "Rényi test"

From Encyclopedia of Mathematics
Jump to: navigation, search
m (tex encoded by computer)
m (Undo revision 48598 by Ulf Rehmann (talk))
Tag: Undo
Line 1: Line 1:
−
<!--
+
A [[Statistical test|statistical test]] used for testing a simple non-parametric hypothesis <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r081/r081270/r0812701.png" /> (cf. [[Non-parametric methods in statistics|Non-parametric methods in statistics]]), according to which independent identically-distributed random variables <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r081/r081270/r0812702.png" /> have a given continuous distribution function <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r081/r081270/r0812703.png" />, against the alternatives:
−
r0812701.png
 
−
$#A+1 = 55 n = 0
 
−
$#C+1 = 55 : ~/encyclopedia/old_files/data/R081/R.0801270 R\Aeenyi test
 
−
Automatically converted into TeX, above some diagnostics.
 
−
Please remove this comment and the {{TEX|auto}} line below,
 
−
if TeX found to be correct.
 
−
-->
 
  
−
{{TEX|auto}}
+
<table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r081/r081270/r0812704.png" /></td> </tr></table>
−
{{TEX|done}}
 
  
−
A [[Statistical test|statistical test]] used for testing a simple non-parametric hypothesis  $  H _ {0} $(
+
<table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r081/r081270/r0812705.png" /></td> </tr></table>
−
cf. [[Non-parametric methods in statistics|Non-parametric methods in statistics]]), according to which independent identically-distributed random variables  $  X _ {1} \dots X _ {n} $
 
−
have a given continuous distribution function  $  F( x) $,
 
−
against the alternatives:
 
  
−
$$
+
<table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r081/r081270/r0812706.png" /></td> </tr></table>
−
H _ {1}  ^ {+} : \sup _ {| x | < \infty }  \psi [ F( x)] ( {\mathsf E} F _ {n} ( x) - F( x))
 
−
> 0,
 
−
$$
 
  
−
$$
+
where <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r081/r081270/r0812707.png" /> is the empirical distribution function constructed with respect to the sample <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r081/r081270/r0812708.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r081/r081270/r0812709.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r081/r081270/r08127010.png" />, is a weight function. If
−
H _ {1}  ^ {-} : \inf _ {| x | <
 
−
\infty }  \psi [ F( x)]( {\mathsf E} F _ {n} ( x) - F( x))  < 0,
 
−
$$
 
  
−
$$
+
<table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r081/r081270/r08127011.png" /></td> </tr></table>
−
H _ {1} : \sup _ {| x | < \infty } \
 
−
\psi [ F( x)] | {\mathsf E} F _ {n} ( x) - F( x) |  > 0,
 
−
$$
 
  
−
where $  F _ {n} ( x) $
+
where <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r081/r081270/r08127012.png" /> is any fixed number from the interval <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r081/r081270/r08127013.png" />, then the Rényi test, which was intended for testing <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r081/r081270/r08127014.png" /> against the alternatives <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r081/r081270/r08127015.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r081/r081270/r08127016.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r081/r081270/r08127017.png" />, is based on the Rényi statistics
−
is the empirical distribution function constructed with respect to the sample  $  X _ {1} \dots X _ {n} $
 
−
and  $  \psi ( F  ) $,  
 
−
$  \psi \geq  0 $,  
 
−
is a weight function. If
 
  
−
$$
+
<table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r081/r081270/r08127018.png" /></td> </tr></table>
−
\psi [ F( x)]  = \left \{
 
  
−
where  $  a $
+
<table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r081/r081270/r08127019.png" /></td> </tr></table>
−
is any fixed number from the interval  $  [ 0, 1] $,
 
−
then the Rényi test, which was intended for testing  $  H _ {0} $
 
−
against the alternatives  $  H _ {1}  ^ {+} $,
 
−
$  H _ {1}  ^ {-} $,
 
−
$  H _ {1} $,
 
−
is based on the Rényi statistics
 
  
−
$$
+
<table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r081/r081270/r08127020.png" /></td> </tr></table>
−
R _ {n}  ^ {+} ( a, 1)  = \
 
−
\sup _ {F( x) \geq  a } 
 
−
\frac{F _ {n} ( x) - F( x) }{F(}
 
−
x) =
 
−
$$
 
  
−
$$
+
<table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r081/r081270/r08127021.png" /></td> </tr></table>
−
= \
 
−
\max _ {F( X _ {(} m) ) \geq  a } 
 
−
\frac{( m / n) - F( X _ {(} m) ) }{F( X _ {(} m) ) }
 
−
,
 
−
$$
 
  
−
$$
+
<table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r081/r081270/r08127022.png" /></td> </tr></table>
−
R _ {n}  ^ {-} ( a, 1)  = - \inf _ {F( x)
 
−
\geq  a } 
 
−
\frac{F _ {n} ( x) - F( x) }{F(}
 
−
x) =
 
−
$$
 
  
−
$$
+
<table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r081/r081270/r08127023.png" /></td> </tr></table>
−
= \
 
−
\max _ {F( X _ {(} m) ) \geq  a } 
 
−
\frac{F( X _ {(} m) ) - ( m- 1) / n }{F( X _ {(} m) ) }
 
−
,
 
−
$$
 
  
−
$$
+
where <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r081/r081270/r08127024.png" /> are the members of the series of order statistics
−
R _ {n} ( a, 1)  = \sup _ {F( x) \geq  a } 
 
−
\frac{| F _ {n} ( x) - F( x) | }{F(}
 
−
x) =
 
−
$$
 
  
−
$$
+
<table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r081/r081270/r08127025.png" /></td> </tr></table>
−
= \
 
−
\max \{ R _ {n}  ^ {+} ( a, 1), R _ {n}  ^ {-} ( a, 1) \} ,
 
−
$$
 
  
−
where  $  X _ {(} 1) \dots X _ {(} n) $
+
constructed with respect to the observations <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r081/r081270/r08127026.png" />.
−
are the members of the series of order statistics
 
  
−
$$
+
The statistics <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r081/r081270/r08127027.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r081/r081270/r08127028.png" /> satisfy the same probability law and, if <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r081/r081270/r08127029.png" />, then
−
X _ {(} 1)  \leq  \dots \leq  X _ {(} n) ,
 
−
$$
 
  
−
constructed with respect to the observations  $  X _ {1} \dots X _ {n} $.
+
<table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r081/r081270/r08127030.png" /></td> <td valign="top" style="width:5%;text-align:right;">(1)</td></tr></table>
  
−
The statistics  $  R _ {n}  ^ {+} ( a, 1) $
+
<table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r081/r081270/r08127031.png" /></td> <td valign="top" style="width:5%;text-align:right;">(2)</td></tr></table>
−
and  $  R _ {n}  ^ {-} ( a, 1) $
 
−
satisfy the same probability law and, if  $  0 < a \leq  1 $,
 
−
then
 
  
−
$$ \tag{1 }
+
where <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r081/r081270/r08127032.png" /> is the distribution function of the standard normal law (cf. [[Normal distribution|Normal distribution]]) and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r081/r081270/r08127033.png" /> is the Rényi distribution function,
−
\lim\limits _ {n \rightarrow \infty }  {\mathsf P} \left \{ \sqrt {
 
−
\frac{na}{1-}
 
−
a } R _ {n}  ^ {+} ( a, 1) <
 
−
x \right \}  = \
 
−
2 \Phi ( x) - 1,\  x > 0,
 
−
$$
 
  
−
$$ \tag{2 }
+
<table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r081/r081270/r08127034.png" /></td> </tr></table>
−
\lim\limits _ {n \rightarrow \infty }  {\mathsf P} \left \{ \sqrt {
 
−
\frac{na}{1-}
 
−
a
 
−
} R _ {n} ( a, 1) < x \right \}  = L( x),\  x > 0,
 
−
$$
 
  
−
where  $  \Phi ( x) $
+
If <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r081/r081270/r08127035.png" />, then
−
is the distribution function of the standard normal law (cf. [[Normal distribution|Normal distribution]]) and  $  L( x) $
 
−
is the Rényi distribution function,
 
  
−
$$
+
<table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r081/r081270/r08127036.png" /></td> </tr></table>
−
L( x)  =
 
−
\frac{4} \pi
 
−
\sum _ { k= } 0 ^  \infty 
 
−
\frac{(- 1)  ^ {k} }{2k+}
 
−
1  \mathop{\rm exp} \left \{ -
 
  
−
\frac{( 2k+ 1) ^ {2} \pi  ^ {2} }{8x  ^ {2} }
+
It follows from (1) and (2) that for larger values of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r081/r081270/r08127037.png" /> the following approximate values may be used to calculate the <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r081/r081270/r08127038.png" />-percent critical values <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r081/r081270/r08127039.png" /> for the statistics <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r081/r081270/r08127040.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r081/r081270/r08127041.png" />:
−
\right \} .
 
−
$$
 
  
−
If  $  a = 0 $,
+
<table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r081/r081270/r08127042.png" /></td> </tr></table>
−
then
 
  
−
$$
+
respectively, where <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r081/r081270/r08127043.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r081/r081270/r08127044.png" /> are the inverse functions to <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r081/r081270/r08127045.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r081/r081270/r08127046.png" />, respectively. This means that if <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r081/r081270/r08127047.png" />, then <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r081/r081270/r08127048.png" />.
−
{\mathsf P} \{ R _ {n}  ^ {+} ( 0, 1) \geq  x \}  = \
 
−
1 -
 
−
\frac{x}{1+}
 
−
x ,\  x > 0.
 
−
$$
 
  
−
It follows from (1) and (2) that for larger values of  $  n $
+
Furthermore, if <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r081/r081270/r08127049.png" />, then it is advisable to use the approximate equation
−
the following approximate values may be used to calculate the  $  Q $-
 
−
percent critical values  $  ( 0\pct< Q < 50\pct) $
 
−
for the statistics  $  R _ {n}  ^ {+} ( a, 1) $
 
−
and  $  R _ {n} ( a, 1) $:
 
  
−
$$
+
<table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r081/r081270/r08127050.png" /></td> </tr></table>
−
\sqrt {1-
 
−
\frac{a}{na}
 
−
} \Phi  ^ {-} 1 ( 1 - 0.005 Q) \  \textrm{ and } \ \
 
−
\sqrt {1-
 
−
\frac{a}{na}
 
−
} L  ^ {-} 1 ( 1 - 0.01 Q) ,
 
−
$$
 
  
−
respectively, where  $  \Phi  ^ {-} 1 ( x) $
+
when calculating the values of the Rényi distribution function <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r081/r081270/r08127051.png" />; its degree of error does not exceed <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r081/r081270/r08127052.png" />.
−
and  $  L  ^ {-} 1 ( x) $
 
−
are the inverse functions to  $  \Phi ( x) $
 
−
and  $  L( x) $,
 
−
respectively. This means that if  $  0\pct < Q < 10\pct $,
 
−
then  $  \Phi  ^ {-} 1 ( 1 - 0.005Q) \approx L  ^ {-} 1 ( 1 - 0.02Q) $.
 
−
 
 
−
Furthermore, if  $  x > 2.99 $,
 
−
then it is advisable to use the approximate equation
 
−
 
 
−
$$
 
−
L( x)  \approx  4 \Phi ( x) - 3
 
−
$$
 
−
 
 
−
when calculating the values of the Rényi distribution function $  L( x) $;  
 
−
its degree of error does not exceed $  5 \cdot 10  ^ {-} 7 $.
 
  
 
In addition to the Rényi test discused here, there are also similar tests, corresponding to the weight function
 
In addition to the Rényi test discused here, there are also similar tests, corresponding to the weight function
  
−
$$
+
<table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r081/r081270/r08127053.png" /></td> </tr></table>
−
\phi [ F( x)]  = \left \{
 
  
−
where $  a $
+
where <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r081/r081270/r08127054.png" /> is any fixed number from the interval <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r081/r081270/r08127055.png" />.
−
is any fixed number from the interval $  [ 0, 1] $.
 
  
 
====References====
 
====References====
 
<table><TR><TD valign="top">[1]</TD> <TD valign="top">  A. Rényi,  "On the theory of order statistics"  ''Acta Math. Acad. Sci. Hungar.'' , '''4'''  (1953)  pp. 191–231</TD></TR><TR><TD valign="top">[2]</TD> <TD valign="top">  J. Hájek,  Z. Sidák,  "Theory of rank tests" , Acad. Press  (1967)</TD></TR><TR><TD valign="top">[3]</TD> <TD valign="top">  L.N. Bol'shev,  N.V. Smirnov,  "Tables of mathematical statistics" , ''Libr. math. tables'' , '''46''' , Nauka  (1983)  (In Russian)  (Processed by L.S. Bark and E.S. Kedrova)</TD></TR></table>
 
<table><TR><TD valign="top">[1]</TD> <TD valign="top">  A. Rényi,  "On the theory of order statistics"  ''Acta Math. Acad. Sci. Hungar.'' , '''4'''  (1953)  pp. 191–231</TD></TR><TR><TD valign="top">[2]</TD> <TD valign="top">  J. Hájek,  Z. Sidák,  "Theory of rank tests" , Acad. Press  (1967)</TD></TR><TR><TD valign="top">[3]</TD> <TD valign="top">  L.N. Bol'shev,  N.V. Smirnov,  "Tables of mathematical statistics" , ''Libr. math. tables'' , '''46''' , Nauka  (1983)  (In Russian)  (Processed by L.S. Bark and E.S. Kedrova)</TD></TR></table>

Revision as of 14:53, 7 June 2020

A statistical test used for testing a simple non-parametric hypothesis 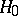(cf. Non-parametric methods in statistics), according to which independent identically-distributed random variables 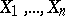have a given continuous distribution function 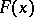, against the alternatives:

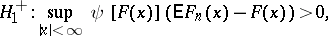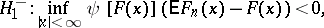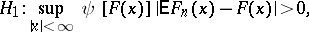where 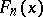is the empirical distribution function constructed with respect to the sample 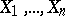and 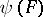, , 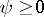is a weight function. If

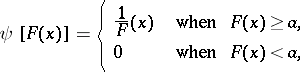where is any fixed number from the interval 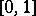, then the Rényi test, which was intended for testing 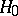against the alternatives 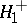, , 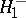, 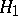is based on the Rényi statistics

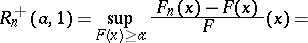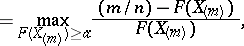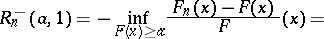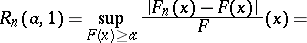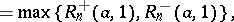where 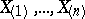are the members of the series of order statistics

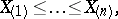constructed with respect to the observations .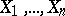

The statistics 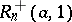and 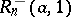satisfy the same probability law and, if 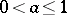, then

(1)
(2)

where 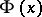is the distribution function of the standard normal law (cf. Normal distribution) and 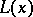is the Rényi distribution function,

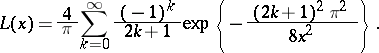If 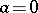, then

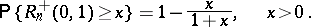It follows from (1) and (2) that for larger values of the following approximate values may be used to calculate the 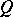-percent critical values 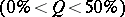for the statistics 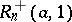and :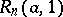

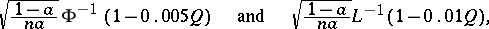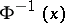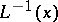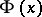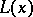respectively, where and are the inverse functions to and , respectively. This means that if 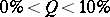, then .

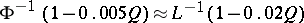Furthermore, if 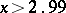, then it is advisable to use the approximate equation

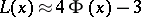when calculating the values of the Rényi distribution function 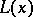; its degree of error does not exceed .

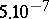In addition to the Rényi test discused here, there are also similar tests, corresponding to the weight function

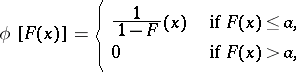where is any fixed number from the interval .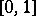

References

[1] A. Rényi, "On the theory of order statistics" Acta Math. Acad. Sci. Hungar. , 4 (1953) pp. 191–231
[2] J. Hájek, Z. Sidák, "Theory of rank tests" , Acad. Press (1967)
[3] L.N. Bol'shev, N.V. Smirnov, "Tables of mathematical statistics" , Libr. math. tables , 46 , Nauka (1983) (In Russian) (Processed by L.S. Bark and E.S. Kedrova)
How to Cite This Entry:
Rényi test. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=R%C3%A9nyi_test&oldid=48598
This article was adapted from an original article by M.S. Nikulin (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098. See original article
Retrieved from "https://encyclopediaofmath.org/index.php?title=Rényi_test&oldid=49414"