Difference between revisions of "Rotation"
Ulf Rehmann (talk | contribs) m (tex encoded by computer) |
Ulf Rehmann (talk | contribs) m (Undo revision 48587 by Ulf Rehmann (talk)) Tag: Undo |
||
| Line 1: | Line 1: | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
A special kind of [[Motion|motion]], for which at least one point in space remains at rest. If the rotation is in a plane, the fixed point is called the centre of the rotation; if the rotation is in space, the fixed straight line is called the axis of rotation. A rotation in a Euclidean space is called proper (a rotation of the first kind) or improper (a rotation of the second kind) depending on whether or not the [[Orientation|orientation]] in space remains unchanged. | A special kind of [[Motion|motion]], for which at least one point in space remains at rest. If the rotation is in a plane, the fixed point is called the centre of the rotation; if the rotation is in space, the fixed straight line is called the axis of rotation. A rotation in a Euclidean space is called proper (a rotation of the first kind) or improper (a rotation of the second kind) depending on whether or not the [[Orientation|orientation]] in space remains unchanged. | ||
| − | A proper rotation in a plane can be analytically expressed in Cartesian orthogonal coordinates | + | A proper rotation in a plane can be analytically expressed in Cartesian orthogonal coordinates <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r082/r082620/r0826201.png" /> by the formulas |
| − | by the formulas | ||
| − | + | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r082/r082620/r0826202.png" /></td> </tr></table> | |
| − | |||
| − | |||
| − | |||
| − | where | + | where <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r082/r082620/r0826203.png" /> is the rotation angle and the centre of the rotation is the coordinate origin. A proper rotation through an angle <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r082/r082620/r0826204.png" /> may be represented as the product of two axial symmetries (reflections, cf. [[Reflection|Reflection]]) with axes forming an angle of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r082/r082620/r0826205.png" /> with each other. An improper rotation in a plane can be analytically expressed in Cartesian orthogonal coordinates <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r082/r082620/r0826206.png" /> by the formulas |
| − | is the rotation angle and the centre of the rotation is the coordinate origin. A proper rotation through an angle | ||
| − | may be represented as the product of two axial symmetries (reflections, cf. [[Reflection|Reflection]]) with axes forming an angle of | ||
| − | with each other. An improper rotation in a plane can be analytically expressed in Cartesian orthogonal coordinates | ||
| − | by the formulas | ||
| − | + | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r082/r082620/r0826207.png" /></td> </tr></table> | |
| − | |||
| − | |||
| − | |||
| − | where | + | where <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r082/r082620/r0826208.png" /> is the rotation angle and the centre of the rotation is the coordinate origin. An improper rotation in a plane may be represented as a product of a proper rotation by an axial symmetry. |
| − | is the rotation angle and the centre of the rotation is the coordinate origin. An improper rotation in a plane may be represented as a product of a proper rotation by an axial symmetry. | ||
| − | A rotation in an | + | A rotation in an <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r082/r082620/r0826209.png" />-dimensional Euclidean space can be analytically expressed by an [[Orthogonal matrix|orthogonal matrix]] in canonical form: |
| − | dimensional Euclidean space can be analytically expressed by an [[Orthogonal matrix|orthogonal matrix]] in canonical form: | ||
| − | + | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r082/r082620/r08262010.png" /></td> </tr></table> | |
| − | |||
where | where | ||
| − | + | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r082/r082620/r08262011.png" /></td> </tr></table> | |
| − | |||
| − | |||
| − | + | <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r082/r082620/r08262012.png" /> is the identity matrix of order <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r082/r082620/r08262013.png" /> (<img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r082/r082620/r08262014.png" />). The following cases are possible: | |
| − | is the identity matrix of order | ||
| − | |||
| − | The following cases are possible: | ||
| − | 1) | + | 1) <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r082/r082620/r08262015.png" /> — the identity transformation; |
| − | the identity transformation; | ||
| − | 2) | + | 2) <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r082/r082620/r08262016.png" /> — the rotation is a central symmetry; |
| − | the rotation is a central symmetry; | ||
| − | 3) | + | 3) <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r082/r082620/r08262017.png" /> — the rotation is a symmetry with respect to a <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r082/r082620/r08262018.png" />-plane (a reflection in a <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r082/r082620/r08262019.png" />-plane); |
| − | the rotation is a symmetry with respect to a | ||
| − | plane (a reflection in a | ||
| − | plane); | ||
| − | 4) | + | 4) <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r082/r082620/r08262020.png" /> does not contain submatrices <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r082/r082620/r08262021.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r082/r082620/r08262022.png" /> — the rotation is called a rotation around a unique fixed point; |
| − | does not contain submatrices | ||
| − | and | ||
| − | the rotation is called a rotation around a unique fixed point; | ||
| − | 5) | + | 5) <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r082/r082620/r08262023.png" /> contains the submatrices <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r082/r082620/r08262024.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r082/r082620/r08262025.png" /> but does not contain the submatrix <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r082/r082620/r08262026.png" /> — the rotation is a rotation around a <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r082/r082620/r08262028.png" />-plane; |
| − | contains the submatrices | ||
| − | and | ||
| − | but does not contain the submatrix | ||
| − | the rotation is a rotation around a | ||
| − | plane; | ||
| − | 6) | + | 6) <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r082/r082620/r08262029.png" /> contains the submatrices <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r082/r082620/r08262030.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r082/r082620/r08262031.png" /> but does not contain the submatrix <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r082/r082620/r08262032.png" /> — the rotation is called a rotational reflection in an <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r082/r082620/r08262034.png" />-plane. |
| − | contains the submatrices | ||
| − | and | ||
| − | but does not contain the submatrix | ||
| − | the rotation is called a rotational reflection in an | ||
| − | plane. | ||
| − | The rotations of a Euclidean space around a given point form a group with respect to multiplication of rotations. This group is isomorphic to the group of orthogonal transformations (cf. [[Orthogonal transformation|Orthogonal transformation]]) of the vector space | + | The rotations of a Euclidean space around a given point form a group with respect to multiplication of rotations. This group is isomorphic to the group of orthogonal transformations (cf. [[Orthogonal transformation|Orthogonal transformation]]) of the vector space <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r082/r082620/r08262035.png" /> or to the group of orthogonal matrices of order <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r082/r082620/r08262036.png" /> over the field <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r082/r082620/r08262037.png" />. The rotation group of the space <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r082/r082620/r08262038.png" /> is an <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r082/r082620/r08262039.png" />-dimensional Lie group with an intransitive action on <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r082/r082620/r08262040.png" />. |
| − | or to the group of orthogonal matrices of order | ||
| − | over the field | ||
| − | The rotation group of the space | ||
| − | is an | ||
| − | dimensional Lie group with an intransitive action on | ||
====References==== | ====References==== | ||
<table><TR><TD valign="top">[1]</TD> <TD valign="top"> B.A. Rozenfel'd, "Multi-dimensional spaces" , Moscow (1966) (In Russian)</TD></TR><TR><TD valign="top">[2]</TD> <TD valign="top"> B.A. Rozenfel'd, "Non-Euclidean spaces" , Moscow (1969) (In Russian)</TD></TR><TR><TD valign="top">[3]</TD> <TD valign="top"> P.A. Shirokov, "Tensor calculus. Tensor algebra" , Kazan' (1961) (In Russian)</TD></TR></table> | <table><TR><TD valign="top">[1]</TD> <TD valign="top"> B.A. Rozenfel'd, "Multi-dimensional spaces" , Moscow (1966) (In Russian)</TD></TR><TR><TD valign="top">[2]</TD> <TD valign="top"> B.A. Rozenfel'd, "Non-Euclidean spaces" , Moscow (1969) (In Russian)</TD></TR><TR><TD valign="top">[3]</TD> <TD valign="top"> P.A. Shirokov, "Tensor calculus. Tensor algebra" , Kazan' (1961) (In Russian)</TD></TR></table> | ||
| + | |||
| + | |||
====Comments==== | ====Comments==== | ||
| + | |||
====References==== | ====References==== | ||
<table><TR><TD valign="top">[a1]</TD> <TD valign="top"> M. Berger, "Geometry" , '''I''' , Springer (1987)</TD></TR><TR><TD valign="top">[a2]</TD> <TD valign="top"> H.S.M. Coxeter, "Introduction to geometry" , Wiley (1963)</TD></TR><TR><TD valign="top">[a3]</TD> <TD valign="top"> M. Greenberg, "Euclidean and non-Euclidean geometry" , Freeman (1980) pp. 105</TD></TR><TR><TD valign="top">[a4]</TD> <TD valign="top"> B.A. [B.A. Rozenfel'd] Rosenfel'd, "A history of non-euclidean geometry" , Springer (1988) (Translated from Russian)</TD></TR><TR><TD valign="top">[a5]</TD> <TD valign="top"> B. Artmann, "Lineare Algebra" , Birkhäuser (1986)</TD></TR><TR><TD valign="top">[a6]</TD> <TD valign="top"> P.R. Halmos, "Finite-dimensional vector spaces" , v. Nostrand (1958)</TD></TR></table> | <table><TR><TD valign="top">[a1]</TD> <TD valign="top"> M. Berger, "Geometry" , '''I''' , Springer (1987)</TD></TR><TR><TD valign="top">[a2]</TD> <TD valign="top"> H.S.M. Coxeter, "Introduction to geometry" , Wiley (1963)</TD></TR><TR><TD valign="top">[a3]</TD> <TD valign="top"> M. Greenberg, "Euclidean and non-Euclidean geometry" , Freeman (1980) pp. 105</TD></TR><TR><TD valign="top">[a4]</TD> <TD valign="top"> B.A. [B.A. Rozenfel'd] Rosenfel'd, "A history of non-euclidean geometry" , Springer (1988) (Translated from Russian)</TD></TR><TR><TD valign="top">[a5]</TD> <TD valign="top"> B. Artmann, "Lineare Algebra" , Birkhäuser (1986)</TD></TR><TR><TD valign="top">[a6]</TD> <TD valign="top"> P.R. Halmos, "Finite-dimensional vector spaces" , v. Nostrand (1958)</TD></TR></table> | ||
Revision as of 14:53, 7 June 2020
A special kind of motion, for which at least one point in space remains at rest. If the rotation is in a plane, the fixed point is called the centre of the rotation; if the rotation is in space, the fixed straight line is called the axis of rotation. A rotation in a Euclidean space is called proper (a rotation of the first kind) or improper (a rotation of the second kind) depending on whether or not the orientation in space remains unchanged.
A proper rotation in a plane can be analytically expressed in Cartesian orthogonal coordinates 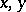 by the formulas
by the formulas
 |
where 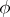 is the rotation angle and the centre of the rotation is the coordinate origin. A proper rotation through an angle
is the rotation angle and the centre of the rotation is the coordinate origin. A proper rotation through an angle 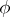 may be represented as the product of two axial symmetries (reflections, cf. Reflection) with axes forming an angle of
may be represented as the product of two axial symmetries (reflections, cf. Reflection) with axes forming an angle of 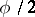 with each other. An improper rotation in a plane can be analytically expressed in Cartesian orthogonal coordinates
with each other. An improper rotation in a plane can be analytically expressed in Cartesian orthogonal coordinates 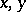 by the formulas
by the formulas
 |
where 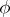 is the rotation angle and the centre of the rotation is the coordinate origin. An improper rotation in a plane may be represented as a product of a proper rotation by an axial symmetry.
is the rotation angle and the centre of the rotation is the coordinate origin. An improper rotation in a plane may be represented as a product of a proper rotation by an axial symmetry.
A rotation in an  -dimensional Euclidean space can be analytically expressed by an orthogonal matrix in canonical form:
-dimensional Euclidean space can be analytically expressed by an orthogonal matrix in canonical form:
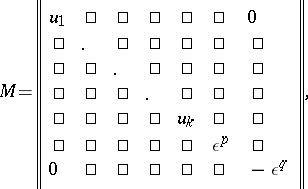 |
where
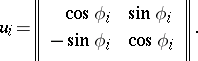 |
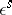 is the identity matrix of order
is the identity matrix of order  (
(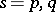 ). The following cases are possible:
). The following cases are possible:
1)  — the identity transformation;
— the identity transformation;
2) 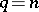 — the rotation is a central symmetry;
— the rotation is a central symmetry;
3) 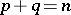 — the rotation is a symmetry with respect to a
— the rotation is a symmetry with respect to a 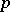 -plane (a reflection in a
-plane (a reflection in a 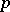 -plane);
-plane);
4) 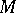 does not contain submatrices
does not contain submatrices 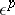 and
and 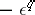 — the rotation is called a rotation around a unique fixed point;
— the rotation is called a rotation around a unique fixed point;
5) 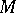 contains the submatrices
contains the submatrices 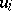 and
and 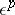 but does not contain the submatrix
but does not contain the submatrix 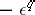 — the rotation is a rotation around a
— the rotation is a rotation around a 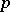 -plane;
-plane;
6) 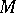 contains the submatrices
contains the submatrices 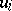 and
and 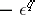 but does not contain the submatrix
but does not contain the submatrix 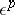 — the rotation is called a rotational reflection in an
— the rotation is called a rotational reflection in an 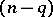 -plane.
-plane.
The rotations of a Euclidean space around a given point form a group with respect to multiplication of rotations. This group is isomorphic to the group of orthogonal transformations (cf. Orthogonal transformation) of the vector space 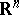 or to the group of orthogonal matrices of order
or to the group of orthogonal matrices of order  over the field
over the field 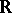 . The rotation group of the space
. The rotation group of the space 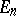 is an
is an 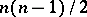 -dimensional Lie group with an intransitive action on
-dimensional Lie group with an intransitive action on 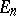 .
.
References
| [1] | B.A. Rozenfel'd, "Multi-dimensional spaces" , Moscow (1966) (In Russian) |
| [2] | B.A. Rozenfel'd, "Non-Euclidean spaces" , Moscow (1969) (In Russian) |
| [3] | P.A. Shirokov, "Tensor calculus. Tensor algebra" , Kazan' (1961) (In Russian) |
Comments
References
| [a1] | M. Berger, "Geometry" , I , Springer (1987) |
| [a2] | H.S.M. Coxeter, "Introduction to geometry" , Wiley (1963) |
| [a3] | M. Greenberg, "Euclidean and non-Euclidean geometry" , Freeman (1980) pp. 105 |
| [a4] | B.A. [B.A. Rozenfel'd] Rosenfel'd, "A history of non-euclidean geometry" , Springer (1988) (Translated from Russian) |
| [a5] | B. Artmann, "Lineare Algebra" , Birkhäuser (1986) |
| [a6] | P.R. Halmos, "Finite-dimensional vector spaces" , v. Nostrand (1958) |
Rotation. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Rotation&oldid=48587