Difference between revisions of "Romberg method"
Ulf Rehmann (talk | contribs) m (tex encoded by computer) |
Ulf Rehmann (talk | contribs) m (Undo revision 48584 by Ulf Rehmann (talk)) Tag: Undo |
||
| Line 1: | Line 1: | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
''Romberg rule'' | ''Romberg rule'' | ||
| − | A method for calculating a definite integral based on [[Richardson extrapolation|Richardson extrapolation]]. Suppose a value | + | A method for calculating a definite integral based on [[Richardson extrapolation|Richardson extrapolation]]. Suppose a value <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r082/r082570/r0825701.png" /> of some functional is to be calculated; also, let a calculated approximate value <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r082/r082570/r0825702.png" /> depend on a parameter <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r082/r082570/r0825703.png" /> so that as a result of the computations one obtains an approximate equality <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r082/r082570/r0825704.png" />. Let some information be known concerning the behaviour of the difference <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r082/r082570/r0825705.png" /> as a function of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r082/r082570/r0825706.png" />, namely, |
| − | of some functional is to be calculated; also, let a calculated approximate value | ||
| − | depend on a parameter | ||
| − | so that as a result of the computations one obtains an approximate equality | ||
| − | Let some information be known concerning the behaviour of the difference | ||
| − | as a function of | ||
| − | namely, | ||
| − | + | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r082/r082570/r0825707.png" /></td> <td valign="top" style="width:5%;text-align:right;">(1)</td></tr></table> | |
| − | |||
| − | |||
| − | where | + | where <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r082/r082570/r0825708.png" /> is a positive integer and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r082/r082570/r0825709.png" /> depends on the functional to be approximated, on the function on which this functional is calculated, on the approximating method, and (weakly) on <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r082/r082570/r08257010.png" />. If simultaneously with <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r082/r082570/r08257011.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r082/r082570/r08257012.png" /> is calculated, then by Richardson's method one obtains for <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r082/r082570/r08257013.png" /> the approximation |
| − | is a positive integer and | ||
| − | depends on the functional to be approximated, on the function on which this functional is calculated, on the approximating method, and (weakly) on | ||
| − | If simultaneously with | ||
| − | |||
| − | is calculated, then by Richardson's method one obtains for | ||
| − | the approximation | ||
| − | + | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r082/r082570/r08257014.png" /></td> <td valign="top" style="width:5%;text-align:right;">(2)</td></tr></table> | |
| − | |||
| − | + | This approximation is the better, the weaker the dependence of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r082/r082570/r08257015.png" /> in (1) on <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r082/r082570/r08257016.png" />. In particular, if <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r082/r082570/r08257017.png" /> is independent of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r082/r082570/r08257018.png" />, then (2) becomes an exact equality. | |
| − | |||
| − | |||
| − | |||
| − | This approximation is the better, the weaker the dependence of | ||
| − | in (1) on | ||
| − | In particular, if | ||
| − | is independent of | ||
| − | then (2) becomes an exact equality. | ||
Romberg's method is used to calculate an integral | Romberg's method is used to calculate an integral | ||
| − | + | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r082/r082570/r08257019.png" /></td> </tr></table> | |
| − | |||
| − | |||
| − | The interval | + | The interval <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r082/r082570/r08257020.png" /> is chosen to facilitate the writing; it can be any finite interval, however. Let |
| − | is chosen to facilitate the writing; it can be any finite interval, however. Let | ||
| − | + | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r082/r082570/r08257021.png" /></td> <td valign="top" style="width:5%;text-align:right;">(3)</td></tr></table> | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r082/r082570/r08257022.png" /></td> </tr></table> | |
| − | |||
| − | |||
Calculations by Romberg's method reduce to writing down the following table: | Calculations by Romberg's method reduce to writing down the following table: | ||
| − | + | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r082/r082570/r08257023.png" /></td> </tr></table> | |
| − | where in the first column one finds the quadrature sums (3) of the [[Trapezium formula|trapezium formula]]. The elements of the | + | where in the first column one finds the quadrature sums (3) of the [[Trapezium formula|trapezium formula]]. The elements of the <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r082/r082570/r08257024.png" />-nd column are obtained from the elements of the <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r082/r082570/r08257025.png" />-st column by the formula |
| − | nd column are obtained from the elements of the | ||
| − | st column by the formula | ||
| − | + | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r082/r082570/r08257026.png" /></td> <td valign="top" style="width:5%;text-align:right;">(4)</td></tr></table> | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
When writing down the table, the main calculating effort is concerned with calculating the elements of the first column. The calculation of the elements of the following columns is a bit more complicated than the calculation of finite differences. | When writing down the table, the main calculating effort is concerned with calculating the elements of the first column. The calculation of the elements of the following columns is a bit more complicated than the calculation of finite differences. | ||
| − | Each element | + | Each element <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r082/r082570/r08257027.png" /> in the table is a quadrature sum approximating the integral: |
| − | in the table is a quadrature sum approximating the integral: | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r082/r082570/r08257028.png" /></td> <td valign="top" style="width:5%;text-align:right;">(5)</td></tr></table> | |
| − | |||
| − | |||
| − | |||
| − | + | The nodes of the quadrature sum <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r082/r082570/r08257029.png" /> are the points <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r082/r082570/r08257030.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r082/r082570/r08257031.png" />, and its coefficients are positive numbers. The quadrature formula (5) is exact for all polynomials of degree not exceeding <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r082/r082570/r08257032.png" />. | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | Under the assumption that the integrand has a continuous derivative on <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r082/r082570/r08257033.png" /> of order <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r082/r082570/r08257034.png" />, the difference <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r082/r082570/r08257035.png" /> can be represented in the form (1), where <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r082/r082570/r08257036.png" />. Hence it follows that the elements of the <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r082/r082570/r08257037.png" />-nd column, calculated by formula (4), are better Richardson approximations than the elements of the <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r082/r082570/r08257038.png" />-st column. In particular, the following representation is valid for the error of the quadrature trapezium formula | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r082/r082570/r08257039.png" /></td> </tr></table> | |
| − | + | and the Richardson method provides a better approximation to <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r082/r082570/r08257040.png" />: | |
| − | |||
| − | + | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r082/r082570/r08257041.png" /></td> </tr></table> | |
| − | |||
| − | |||
| − | |||
| − | + | <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r082/r082570/r08257042.png" /> turns out to be a quadrature sum of the [[Simpson formula|Simpson formula]], and since for the error of this formula the following representation holds: | |
| − | turns out to be a quadrature sum of the [[Simpson formula|Simpson formula]], and since for the error of this formula the following representation holds: | ||
| − | + | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r082/r082570/r08257043.png" /></td> </tr></table> | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
one can again use the Richardson method, etc. | one can again use the Richardson method, etc. | ||
| − | In Romberg's method, to approximate | + | In Romberg's method, to approximate <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r082/r082570/r08257044.png" /> one takes <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r082/r082570/r08257045.png" />; also, one assumes the continuous derivative <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r082/r082570/r08257046.png" /> on <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r082/r082570/r08257047.png" /> to exist. A tentative idea of the precision of the approximation <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r082/r082570/r08257048.png" /> can be obtained by comparing <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r082/r082570/r08257049.png" /> to <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r082/r082570/r08257050.png" />. |
| − | one takes | ||
| − | also, one assumes the continuous derivative | ||
| − | on | ||
| − | to exist. A tentative idea of the precision of the approximation | ||
| − | can be obtained by comparing | ||
| − | to | ||
This method was for the first time described by W. Romberg [[#References|[1]]]. | This method was for the first time described by W. Romberg [[#References|[1]]]. | ||
Revision as of 14:53, 7 June 2020
Romberg rule
A method for calculating a definite integral based on Richardson extrapolation. Suppose a value  of some functional is to be calculated; also, let a calculated approximate value
of some functional is to be calculated; also, let a calculated approximate value  depend on a parameter
depend on a parameter  so that as a result of the computations one obtains an approximate equality
so that as a result of the computations one obtains an approximate equality  . Let some information be known concerning the behaviour of the difference
. Let some information be known concerning the behaviour of the difference  as a function of
as a function of  , namely,
, namely,
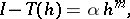 | (1) |
where  is a positive integer and
is a positive integer and  depends on the functional to be approximated, on the function on which this functional is calculated, on the approximating method, and (weakly) on
depends on the functional to be approximated, on the function on which this functional is calculated, on the approximating method, and (weakly) on  . If simultaneously with
. If simultaneously with  ,
, 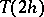 is calculated, then by Richardson's method one obtains for
is calculated, then by Richardson's method one obtains for  the approximation
the approximation
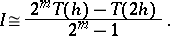 | (2) |
This approximation is the better, the weaker the dependence of 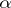 in (1) on
in (1) on 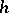 . In particular, if
. In particular, if 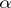 is independent of
is independent of  , then (2) becomes an exact equality.
, then (2) becomes an exact equality.
Romberg's method is used to calculate an integral
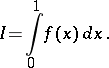 |
The interval 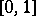 is chosen to facilitate the writing; it can be any finite interval, however. Let
is chosen to facilitate the writing; it can be any finite interval, however. Let
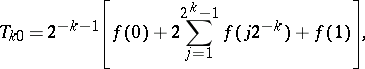 | (3) |
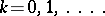 |
Calculations by Romberg's method reduce to writing down the following table:
 |
where in the first column one finds the quadrature sums (3) of the trapezium formula. The elements of the  -nd column are obtained from the elements of the
-nd column are obtained from the elements of the 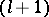 -st column by the formula
-st column by the formula
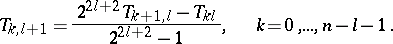 | (4) |
When writing down the table, the main calculating effort is concerned with calculating the elements of the first column. The calculation of the elements of the following columns is a bit more complicated than the calculation of finite differences.
Each element  in the table is a quadrature sum approximating the integral:
in the table is a quadrature sum approximating the integral:
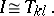 | (5) |
The nodes of the quadrature sum  are the points
are the points 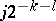 ,
, 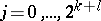 , and its coefficients are positive numbers. The quadrature formula (5) is exact for all polynomials of degree not exceeding
, and its coefficients are positive numbers. The quadrature formula (5) is exact for all polynomials of degree not exceeding 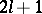 .
.
Under the assumption that the integrand has a continuous derivative on  of order
of order  , the difference
, the difference  can be represented in the form (1), where
can be represented in the form (1), where 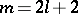 . Hence it follows that the elements of the
. Hence it follows that the elements of the  -nd column, calculated by formula (4), are better Richardson approximations than the elements of the
-nd column, calculated by formula (4), are better Richardson approximations than the elements of the 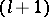 -st column. In particular, the following representation is valid for the error of the quadrature trapezium formula
-st column. In particular, the following representation is valid for the error of the quadrature trapezium formula
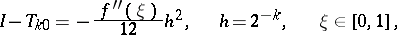 |
and the Richardson method provides a better approximation to  :
:
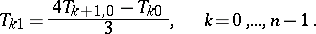 |
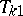 turns out to be a quadrature sum of the Simpson formula, and since for the error of this formula the following representation holds:
turns out to be a quadrature sum of the Simpson formula, and since for the error of this formula the following representation holds:
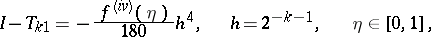 |
one can again use the Richardson method, etc.
In Romberg's method, to approximate 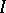 one takes
one takes 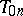 ; also, one assumes the continuous derivative
; also, one assumes the continuous derivative 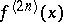 on
on  to exist. A tentative idea of the precision of the approximation
to exist. A tentative idea of the precision of the approximation 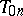 can be obtained by comparing
can be obtained by comparing 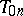 to
to 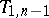 .
.
This method was for the first time described by W. Romberg [1].
References
| [1] | W. Romberg, "Vereinfachte numerische Integration" Norske Vid. Sels. Forh. , 28 : 7 (1955) pp. 30–36 |
| [2] | F.L. Bauer, H. Rutishauser, E. Stiefel, "New aspects in numerical quadrature" N.C. Metropolis (ed.) et al. (ed.) , Experimental Arithmetic, high-speed computing and mathematics , Proc. Symp. Appl. Math. , 15 , Amer. Math. Soc. (1963) pp. 199–218 |
Romberg method. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Romberg_method&oldid=48584