Difference between revisions of "Plücker coordinates"
Ulf Rehmann (talk | contribs) m (tex encoded by computer) |
Ulf Rehmann (talk | contribs) m (Undo revision 48194 by Ulf Rehmann (talk)) Tag: Undo |
||
| Line 1: | Line 1: | ||
| − | < | + | The coordinates of a straight line in three-dimensional space, the six numbers <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p072/p072890/p0728901.png" />, and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p072/p072890/p0728902.png" />, of which the first three are the coordinates of the direction vector <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p072/p072890/p0728903.png" /> for the straight line <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p072/p072890/p0728904.png" /> and the second three are the moments of this vector about the origin. Let the line <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p072/p072890/p0728905.png" /> pass through the points <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p072/p072890/p0728906.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p072/p072890/p0728907.png" /> with projective coordinates <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p072/p072890/p0728908.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p072/p072890/p0728909.png" />, respectively; the Plücker coordinates for this line are the numbers |
| − | p0728901.png | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p072/p072890/p07289010.png" /></td> </tr></table> | |
| − | |||
| − | The coordinates | + | The Plücker coordinates are used in line geometry. They were first considered by J. Plücker (1869). Sometimes, instead of the Plücker coordinates one uses the Klein coordinates <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p072/p072890/p07289011.png" />, which are related to the Plücker ones as follows: |
| − | |||
| − | of | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p072/p072890/p07289012.png" /></td> </tr></table> | |
| − | |||
| − | |||
| − | + | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p072/p072890/p07289013.png" /></td> </tr></table> | |
| − | |||
| − | + | More generally, one naturally considers the Plücker coordinates as coordinates of a <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p072/p072890/p07289014.png" />-dimensional vector subspace of an <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p072/p072890/p07289015.png" />-dimensional vector space <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p072/p072890/p07289016.png" />. Then they are understood as the set of numbers equal to <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p072/p072890/p07289017.png" />-subdeterminants of the <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p072/p072890/p07289018.png" />-matrix <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p072/p072890/p07289019.png" /> with as columns <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p072/p072890/p07289020.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p072/p072890/p07289021.png" />, the coordinate columns (in some basis for <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p072/p072890/p07289022.png" />) of the basis vectors of a subspace <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p072/p072890/p07289023.png" />. If <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p072/p072890/p07289024.png" /> are the components of a column <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p072/p072890/p07289025.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p072/p072890/p07289026.png" />, then the Plücker coordinates (or Grassmann coordinates) are the numbers | |
| − | p | ||
| − | p | ||
| − | p | ||
| − | |||
| − | + | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p072/p072890/p07289027.png" /></td> </tr></table> | |
| − | |||
| − | |||
| − | + | The Plücker coordinates are anti-symmetric in all indices. The number of significant Plücker coordinates is <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p072/p072890/p07289028.png" />. | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | When the basis of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p072/p072890/p07289029.png" /> is changed and the basis for <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p072/p072890/p07289030.png" /> is fixed, the Plücker coordinates are all multiplied by the same non-zero number. When the basis of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p072/p072890/p07289031.png" /> is changed and the basis for <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p072/p072890/p07289032.png" /> is fixed, the Plücker coordinates transform as the components of a contravariant tensor of valency <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p072/p072890/p07289033.png" /> (see [[Poly-vector|Poly-vector]]). Two subspaces coincide if and only if their Plücker coordinates, calculated in the same basis for <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p072/p072890/p07289034.png" />, differ only by a non-zero factor. | |
| − | |||
| − | + | A vector <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p072/p072890/p07289035.png" /> belongs to a subspace <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p072/p072890/p07289036.png" /> if the linear equations | |
| − | + | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p072/p072890/p07289037.png" /></td> </tr></table> | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | with coefficients that are the Plücker coordinates for <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p072/p072890/p07289038.png" />, are fulfilled. In these equations <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p072/p072890/p07289039.png" /> are all possible sets of numbers <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p072/p072890/p07289040.png" />. | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
====Comments==== | ====Comments==== | ||
Relating the Plücker and Klein coordinates as above, the Plücker identity | Relating the Plücker and Klein coordinates as above, the Plücker identity | ||
| − | + | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p072/p072890/p07289041.png" /></td> </tr></table> | |
| − | |||
| − | |||
becomes | becomes | ||
| − | + | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p072/p072890/p07289042.png" /></td> </tr></table> | |
| − | |||
| − | |||
| − | |||
| − | The Plücker coordinates of | + | The Plücker coordinates of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p072/p072890/p07289043.png" />-dimensional subspaces <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p072/p072890/p07289044.png" /> of an <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p072/p072890/p07289045.png" />-dimensional space <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p072/p072890/p07289046.png" /> (over any field) define an imbedding of the Grassmann variety <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p072/p072890/p07289047.png" /> into <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p072/p072890/p07289048.png" />-dimensional projective space <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p072/p072890/p07289049.png" /> with <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p072/p072890/p07289050.png" />. As a subvariety of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p072/p072890/p07289051.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p072/p072890/p07289052.png" /> is given by quadratic relations, the Plücker relations, which look as follows: |
| − | dimensional subspaces | ||
| − | of an | ||
| − | dimensional space | ||
| − | over any field) define an imbedding of the Grassmann variety | ||
| − | into | ||
| − | dimensional projective space | ||
| − | with | ||
| − | As a subvariety of | ||
| − | |||
| − | is given by quadratic relations, the Plücker relations, which look as follows: | ||
| − | + | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p072/p072890/p07289053.png" /></td> </tr></table> | |
| − | |||
| − | |||
| − | |||
| − | i.e. take | + | i.e. take <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p072/p072890/p07289054.png" /> indices <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p072/p072890/p07289055.png" />; <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p072/p072890/p07289056.png" /> and write down the relation above, using that <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p072/p072890/p07289057.png" /> if two of the <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p072/p072890/p07289058.png" />'s are equal. If <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p072/p072890/p07289059.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p072/p072890/p07289060.png" />, there is just one relation: <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p072/p072890/p07289061.png" />. |
| − | indices | ||
| − | |||
| − | and write down the relation above, using that | ||
| − | if two of the | ||
| − | s are equal. If | ||
| − | |||
| − | there is just one relation: | ||
====References==== | ====References==== | ||
<table><TR><TD valign="top">[a1]</TD> <TD valign="top"> H.S.M. Coxeter, "Non-Euclidean geometry" , Univ. Toronto Press (1965) pp. 88–90</TD></TR><TR><TD valign="top">[a2]</TD> <TD valign="top"> B.L. van der Waerden, "Einführung in die algebraische Geometrie" , Springer (1939) pp. Chapt. 1</TD></TR></table> | <table><TR><TD valign="top">[a1]</TD> <TD valign="top"> H.S.M. Coxeter, "Non-Euclidean geometry" , Univ. Toronto Press (1965) pp. 88–90</TD></TR><TR><TD valign="top">[a2]</TD> <TD valign="top"> B.L. van der Waerden, "Einführung in die algebraische Geometrie" , Springer (1939) pp. Chapt. 1</TD></TR></table> | ||
Revision as of 14:52, 7 June 2020
The coordinates of a straight line in three-dimensional space, the six numbers  , and
, and  , of which the first three are the coordinates of the direction vector
, of which the first three are the coordinates of the direction vector  for the straight line
for the straight line  and the second three are the moments of this vector about the origin. Let the line
and the second three are the moments of this vector about the origin. Let the line  pass through the points
pass through the points  and
and  with projective coordinates
with projective coordinates  and
and  , respectively; the Plücker coordinates for this line are the numbers
, respectively; the Plücker coordinates for this line are the numbers
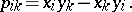 |
The Plücker coordinates are used in line geometry. They were first considered by J. Plücker (1869). Sometimes, instead of the Plücker coordinates one uses the Klein coordinates  , which are related to the Plücker ones as follows:
, which are related to the Plücker ones as follows:
 |
 |
More generally, one naturally considers the Plücker coordinates as coordinates of a  -dimensional vector subspace of an
-dimensional vector subspace of an  -dimensional vector space
-dimensional vector space 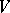 . Then they are understood as the set of numbers equal to
. Then they are understood as the set of numbers equal to  -subdeterminants of the
-subdeterminants of the 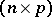 -matrix
-matrix  with as columns
with as columns  ,
,  , the coordinate columns (in some basis for
, the coordinate columns (in some basis for 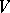 ) of the basis vectors of a subspace
) of the basis vectors of a subspace 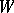 . If
. If  are the components of a column
are the components of a column 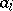 ,
, 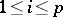 , then the Plücker coordinates (or Grassmann coordinates) are the numbers
, then the Plücker coordinates (or Grassmann coordinates) are the numbers
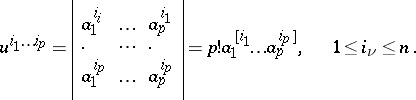 |
The Plücker coordinates are anti-symmetric in all indices. The number of significant Plücker coordinates is  .
.
When the basis of 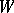 is changed and the basis for
is changed and the basis for  is fixed, the Plücker coordinates are all multiplied by the same non-zero number. When the basis of
is fixed, the Plücker coordinates are all multiplied by the same non-zero number. When the basis of  is changed and the basis for
is changed and the basis for 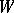 is fixed, the Plücker coordinates transform as the components of a contravariant tensor of valency
is fixed, the Plücker coordinates transform as the components of a contravariant tensor of valency 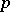 (see Poly-vector). Two subspaces coincide if and only if their Plücker coordinates, calculated in the same basis for
(see Poly-vector). Two subspaces coincide if and only if their Plücker coordinates, calculated in the same basis for 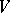 , differ only by a non-zero factor.
, differ only by a non-zero factor.
A vector  belongs to a subspace
belongs to a subspace 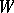 if the linear equations
if the linear equations
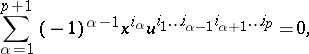 |
with coefficients that are the Plücker coordinates for  , are fulfilled. In these equations
, are fulfilled. In these equations  are all possible sets of numbers
are all possible sets of numbers  .
.
Comments
Relating the Plücker and Klein coordinates as above, the Plücker identity
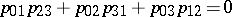 |
becomes
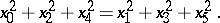 |
The Plücker coordinates of  -dimensional subspaces
-dimensional subspaces 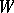 of an
of an  -dimensional space
-dimensional space 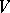 (over any field) define an imbedding of the Grassmann variety
(over any field) define an imbedding of the Grassmann variety  into
into  -dimensional projective space
-dimensional projective space 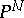 with
with  . As a subvariety of
. As a subvariety of  ,
,  is given by quadratic relations, the Plücker relations, which look as follows:
is given by quadratic relations, the Plücker relations, which look as follows:
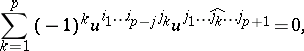 |
i.e. take  indices
indices  ;
; 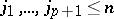 and write down the relation above, using that
and write down the relation above, using that  if two of the
if two of the  's are equal. If
's are equal. If  ,
,  , there is just one relation:
, there is just one relation:  .
.
References
| [a1] | H.S.M. Coxeter, "Non-Euclidean geometry" , Univ. Toronto Press (1965) pp. 88–90 |
| [a2] | B.L. van der Waerden, "Einführung in die algebraische Geometrie" , Springer (1939) pp. Chapt. 1 |
Plücker coordinates. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Pl%C3%BCcker_coordinates&oldid=48194