Namespaces
Variants
Actions

Difference between revisions of "Perron-Frobenius theorem"

From Encyclopedia of Mathematics
Jump to: navigation, search
m (tex encoded by computer)
m (Undo revision 48164 by Ulf Rehmann (talk))
Tag: Undo
Line 1: Line 1:
−
<!--
+
Let a real square <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p072/p072350/p0723501.png" />-matrix <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p072/p072350/p0723502.png" /> be considered as an operator on <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p072/p072350/p0723503.png" />, let it be without invariant coordinate subspaces (such a matrix is called indecomposable) and let it be non-negative (i.e. all its elements are non-negative). Also, let <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p072/p072350/p0723504.png" /> be its eigen values, enumerated such that
−
p0723501.png
 
−
$#A+1 = 20 n = 0
 
−
$#C+1 = 20 : ~/encyclopedia/old_files/data/P072/P.0702350 Perron\ANDFrobenius theorem
 
−
Automatically converted into TeX, above some diagnostics.
 
−
Please remove this comment and the {{TEX|auto}} line below,
 
−
if TeX found to be correct.
 
−
-->
 
  
−
{{TEX|auto}}
+
<table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p072/p072350/p0723505.png" /></td> </tr></table>
−
{{TEX|done}}
 
−
 
 
−
Let a real square  $  ( n \times n) $-
 
−
matrix  $  A $
 
−
be considered as an operator on  $  \mathbf R  ^ {n} $,
 
−
let it be without invariant coordinate subspaces (such a matrix is called indecomposable) and let it be non-negative (i.e. all its elements are non-negative). Also, let  $  \lambda _ {1} \dots \lambda _ {n} $
 
−
be its eigen values, enumerated such that
 
−
 
 
−
$$
 
−
| \lambda _ {1} |  = \dots =  | \lambda _ {h} |  > | \lambda _ {h+} 1 |  \geq  \dots
 
−
\geq  | \lambda _ {n} | ,\ \
 
−
1 \leq  h \leq  n.
 
−
$$
 
  
 
Then,
 
Then,
  
−
1) the number $  r = | \lambda _ {1} | $
+
1) the number <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p072/p072350/p0723506.png" /> is a simple positive root of the [[Characteristic polynomial|characteristic polynomial]] of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p072/p072350/p0723507.png" />;
−
is a simple positive root of the [[Characteristic polynomial|characteristic polynomial]] of $  A $;
 
  
−
2) there exists an eigen vector of $  A $
+
2) there exists an eigen vector of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p072/p072350/p0723508.png" /> with positive coordinates corresponding to <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p072/p072350/p0723509.png" />;
−
with positive coordinates corresponding to $  r $;
 
  
−
3) the numbers $  \lambda _ {1} \dots \lambda _ {h} $
+
3) the numbers <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p072/p072350/p07235010.png" /> coincide, apart from their numbering, with the numbers <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p072/p072350/p07235011.png" />, where <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p072/p072350/p07235012.png" />;
−
coincide, apart from their numbering, with the numbers $  r, \omega r \dots \omega  ^ {h-} 1 r $,  
 
−
where $  \omega = e ^ {2 \pi i/h } $;
 
  
−
4) the product of any eigen value of $  A $
+
4) the product of any eigen value of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p072/p072350/p07235013.png" /> by <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p072/p072350/p07235014.png" /> is an eigen value of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p072/p072350/p07235015.png" />;
−
by $  \omega $
 
−
is an eigen value of $  A $;
 
  
−
5) for $  h > 1 $
+
5) for <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p072/p072350/p07235016.png" /> one can find a permutation of the rows and columns that reduces <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p072/p072350/p07235017.png" /> to the form
−
one can find a permutation of the rows and columns that reduces $  A $
 
−
to the form
 
  
−
$$
+
<table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p072/p072350/p07235018.png" /></td> </tr></table>
−
\left \|
 
  
−
where $  A _ {j} $
+
where <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p072/p072350/p07235019.png" /> is a matrix of order <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p072/p072350/p07235020.png" />.
−
is a matrix of order $  nh  ^ {-} 1 $.
 
  
 
O. Perron proved the assertions 1) and 2) for positive matrices in [[#References|[1]]], while G. Frobenius [[#References|[2]]] gave the full form of the theorem.
 
O. Perron proved the assertions 1) and 2) for positive matrices in [[#References|[1]]], while G. Frobenius [[#References|[2]]] gave the full form of the theorem.
Line 53: Line 23:
 
====References====
 
====References====
 
<table><TR><TD valign="top">[1]</TD> <TD valign="top">  O. Perron,  "Zur Theorie der Matrizen"  ''Math. Ann.'' , '''64'''  (1907)  pp. 248–263</TD></TR><TR><TD valign="top">[2]</TD> <TD valign="top">  G. Frobenius,  "Ueber Matrizen aus nicht negativen Elementen"  ''Sitzungsber. Königl. Preuss. Akad. Wiss.''  (1912)  pp. 456–477</TD></TR><TR><TD valign="top">[3]</TD> <TD valign="top">  F.R. [F.R. Gantmakher] Gantmacher,  "The theory of matrices" , '''1''' , Chelsea, reprint  (1977)  (Translated from Russian)</TD></TR></table>
 
<table><TR><TD valign="top">[1]</TD> <TD valign="top">  O. Perron,  "Zur Theorie der Matrizen"  ''Math. Ann.'' , '''64'''  (1907)  pp. 248–263</TD></TR><TR><TD valign="top">[2]</TD> <TD valign="top">  G. Frobenius,  "Ueber Matrizen aus nicht negativen Elementen"  ''Sitzungsber. Königl. Preuss. Akad. Wiss.''  (1912)  pp. 456–477</TD></TR><TR><TD valign="top">[3]</TD> <TD valign="top">  F.R. [F.R. Gantmakher] Gantmacher,  "The theory of matrices" , '''1''' , Chelsea, reprint  (1977)  (Translated from Russian)</TD></TR></table>
 +
 +
  
 
====Comments====
 
====Comments====

Revision as of 14:52, 7 June 2020

Let a real square 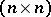-matrix 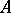be considered as an operator on 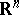, let it be without invariant coordinate subspaces (such a matrix is called indecomposable) and let it be non-negative (i.e. all its elements are non-negative). Also, let be its eigen values, enumerated such that

Then,

1) the number is a simple positive root of the characteristic polynomial of ;

2) there exists an eigen vector of 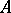with positive coordinates corresponding to ;

3) the numbers coincide, apart from their numbering, with the numbers , where ;

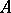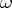4) the product of any eigen value of by is an eigen value of ;

5) for 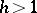one can find a permutation of the rows and columns that reduces to the form

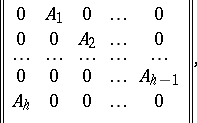where 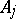is a matrix of order .

O. Perron proved the assertions 1) and 2) for positive matrices in [1], while G. Frobenius [2] gave the full form of the theorem.

References

[1] O. Perron, "Zur Theorie der Matrizen" Math. Ann. , 64 (1907) pp. 248–263
[2] G. Frobenius, "Ueber Matrizen aus nicht negativen Elementen" Sitzungsber. Königl. Preuss. Akad. Wiss. (1912) pp. 456–477
[3] F.R. [F.R. Gantmakher] Gantmacher, "The theory of matrices" , 1 , Chelsea, reprint (1977) (Translated from Russian)


Comments

The Perron–Frobenius theorem has numerous applications, cf. [a1], [a2].

References

[a1] E. Seneta, "Nonnegative matrices" , Allen & Unwin (1973)
[a2] K. Lancaster, "Mathematical economics" , Macmillan (1968)
How to Cite This Entry:
Perron-Frobenius theorem. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Perron-Frobenius_theorem&oldid=48164
This article was adapted from an original article by D.A. Suprunenko (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098. See original article
Retrieved from "https://encyclopediaofmath.org/index.php?title=Perron-Frobenius_theorem&oldid=49363"