Difference between revisions of "Peano derivative"
Ulf Rehmann (talk | contribs) m (tex encoded by computer) |
Ulf Rehmann (talk | contribs) m (Undo revision 48146 by Ulf Rehmann (talk)) Tag: Undo |
||
| Line 1: | Line 1: | ||
| − | < | + | One of the generalizations of the concept of a [[Derivative|derivative]]. Let there exist a <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p071/p071900/p0719001.png" /> such that for all <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p071/p071900/p0719002.png" /> with <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p071/p071900/p0719003.png" /> one has |
| − | p0719001.png | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p071/p071900/p0719004.png" /></td> </tr></table> | |
| − | |||
| − | + | where <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p071/p071900/p0719005.png" /> are constants and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p071/p071900/p0719006.png" /> as <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p071/p071900/p0719007.png" />; let <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p071/p071900/p0719008.png" />. Then <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p071/p071900/p0719009.png" /> is called the generalized Peano derivative of order <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p071/p071900/p07190010.png" /> of the function <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p071/p071900/p07190011.png" /> at the point <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p071/p071900/p07190012.png" />. Symbol: <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p071/p071900/p07190013.png" />; in particular, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p071/p071900/p07190014.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p071/p071900/p07190015.png" />. If <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p071/p071900/p07190016.png" /> exists, then <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p071/p071900/p07190017.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p071/p071900/p07190018.png" />, also exists. If the finite ordinary two-sided derivative <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p071/p071900/p07190019.png" /> exists, then <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p071/p071900/p07190020.png" />. The converse is false for <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p071/p071900/p07190021.png" />: For the function | |
| − | |||
| − | |||
| − | |||
| − | + | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p071/p071900/p07190022.png" /></td> </tr></table> | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | one has <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p071/p071900/p07190023.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p071/p071900/p07190024.png" /> but <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p071/p071900/p07190025.png" /> does not exist for <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p071/p071900/p07190026.png" /> (since <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p071/p071900/p07190027.png" /> is discontinuous for <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p071/p071900/p07190028.png" />). Consequently, the ordinary derivative <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p071/p071900/p07190029.png" /> does not exist for <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p071/p071900/p07190030.png" />. | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | Infinite generalized Peano derivatives have also been introduced. Let for all <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p071/p071900/p07190031.png" /> with <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p071/p071900/p07190032.png" />, | |
| − | |||
| − | + | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p071/p071900/p07190033.png" /></td> </tr></table> | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | where <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p071/p071900/p07190034.png" /> are constants and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p071/p071900/p07190035.png" /> as <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p071/p071900/p07190036.png" /> (<img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p071/p071900/p07190037.png" /> is a number or the symbol <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p071/p071900/p07190038.png" />). Then <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p071/p071900/p07190039.png" /> is also called the Peano derivative of order <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p071/p071900/p07190040.png" /> of the function <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p071/p071900/p07190041.png" /> at the point <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p071/p071900/p07190042.png" />. It was introduced by G. Peano. | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | are constants and | ||
| − | as | ||
| − | |||
| − | is a number or the symbol | ||
| − | Then | ||
| − | is also called the Peano derivative of order | ||
| − | of the function | ||
| − | at the point | ||
| − | It was introduced by G. Peano. | ||
Revision as of 14:52, 7 June 2020
One of the generalizations of the concept of a derivative. Let there exist a 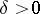 such that for all
such that for all  with
with 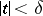 one has
one has
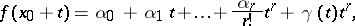 |
where  are constants and
are constants and 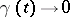 as
as 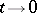 ; let
; let 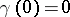 . Then
. Then  is called the generalized Peano derivative of order
is called the generalized Peano derivative of order  of the function
of the function 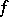 at the point
at the point 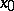 . Symbol:
. Symbol: 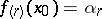 ; in particular,
; in particular, 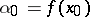 ,
, 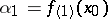 . If
. If 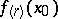 exists, then
exists, then 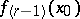 ,
, 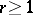 , also exists. If the finite ordinary two-sided derivative
, also exists. If the finite ordinary two-sided derivative 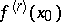 exists, then
exists, then 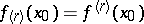 . The converse is false for
. The converse is false for 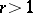 : For the function
: For the function
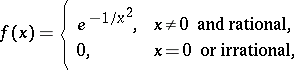 |
one has 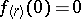 ,
, 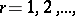 but
but 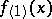 does not exist for
does not exist for 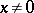 (since
(since 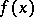 is discontinuous for
is discontinuous for 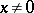 ). Consequently, the ordinary derivative
). Consequently, the ordinary derivative 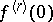 does not exist for
does not exist for 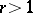 .
.
Infinite generalized Peano derivatives have also been introduced. Let for all 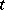 with
with 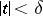 ,
,
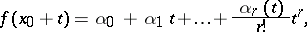 |
where  are constants and
are constants and 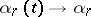 as
as 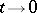 (
(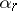 is a number or the symbol
is a number or the symbol 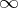 ). Then
). Then 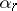 is also called the Peano derivative of order
is also called the Peano derivative of order  of the function
of the function 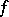 at the point
at the point 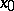 . It was introduced by G. Peano.
. It was introduced by G. Peano.
Peano derivative. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Peano_derivative&oldid=48146