Namespaces
Variants
Actions

Difference between revisions of "Pareto distribution"

From Encyclopedia of Mathematics
Jump to: navigation, search
m (tex encoded by computer)
m (Undo revision 48130 by Ulf Rehmann (talk))
Tag: Undo
Line 1: Line 1:
−
<!--
 
−
p0715801.png
 
−
$#A+1 = 15 n = 0
 
−
$#C+1 = 15 : ~/encyclopedia/old_files/data/P071/P.0701580 Pareto distribution
 
−
Automatically converted into TeX, above some diagnostics.
 
−
Please remove this comment and the {{TEX|auto}} line below,
 
−
if TeX found to be correct.
 
−
-->
 
−
 
−
{{TEX|auto}}
 
−
{{TEX|done}}
 
−
 
 
A continuous [[Probability distribution|probability distribution]] with density
 
A continuous [[Probability distribution|probability distribution]] with density
  
−
$$
+
<table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p071/p071580/p0715801.png" /></td> </tr></table>
−
p( x)  = \left \{
 
−
 
 
−
depending on two parameters  $  x _ {0} > 0 $
 
−
and  $  \alpha > 0 $.
 
−
As a  "cut-off" version the Pareto distribution can be considered as belonging to the family of beta-distributions (cf. [[Beta-distribution|Beta-distribution]]) of the second kind with the density
 
  
−
$$
+
depending on two parameters <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p071/p071580/p0715802.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p071/p071580/p0715803.png" />. As a  "cut-off"  version the Pareto distribution can be considered as belonging to the family of beta-distributions (cf. [[Beta-distribution|Beta-distribution]]) of the second kind with the density
  
−
\frac{1}{B( \mu , \alpha ) }
+
<table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p071/p071580/p0715804.png" /></td> </tr></table>
−
 
−
\frac{x ^ {\mu - 1 } }{( 1+ x) ^ {\mu + \alpha } }
 
−
,\ \
 
−
\mu , \alpha > 0,\ \
 
−
0 < x < \infty ,
 
−
$$
 
  
−
for $  \mu = 1 $.  
+
for <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p071/p071580/p0715805.png" />. For any fixed <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p071/p071580/p0715806.png" />, the Pareto distribution reduces by the transformation <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p071/p071580/p0715807.png" /> to a beta-distribution of the first kind. In the system of [[Pearson curves|Pearson curves]] the Pareto distribution belongs to those of  "type VI"  and  "type XI" . The mathematical expectation of the Pareto distribution is finite for <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p071/p071580/p0715808.png" /> and equal to <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p071/p071580/p0715809.png" />; the variance is finite for <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p071/p071580/p07158010.png" /> and equal to <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p071/p071580/p07158011.png" />; the median is <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p071/p071580/p07158012.png" />. The Pareto distribution function is defined by the formula
−
For any fixed $  x _ {0} $,  
 
−
the Pareto distribution reduces by the transformation $  x = x _ {0} /y $
 
−
to a beta-distribution of the first kind. In the system of [[Pearson curves|Pearson curves]] the Pareto distribution belongs to those of  "type VI"  and  "type XI" . The mathematical expectation of the Pareto distribution is finite for $  \alpha > 1 $
 
−
and equal to $  \alpha x _ {0} /( \alpha - 1) $;  
 
−
the variance is finite for $  \alpha > 2 $
 
−
and equal to $  \alpha x _ {0}  ^ {2} /( \alpha - 1)  ^ {2} ( \alpha - 2) $;  
 
−
the median is $  2 ^ {1/ \alpha } x _ {0} $.  
 
−
The Pareto distribution function is defined by the formula
 
  
−
$$
+
<table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p071/p071580/p07158013.png" /></td> </tr></table>
−
{\mathsf P} \{ X < x \}  = 1 - \left (
 
−
\frac{x _ {0} }{x}
 
−
\right )  ^  \alpha  ,\ \
 
−
x > x _ {0} ,\ \
 
−
\alpha > 0.
 
−
$$
 
  
−
The Pareto distribution has been widely used in various problems of economical statistics, beginning with the work of W. Pareto (1882) on the distribution of profits. It is sometimes accepted that the Pareto distribution describes fairly well the distribution of profits exceeding a certain level in the sense that it must have a tail of order $  1/x  ^  \alpha  $
+
The Pareto distribution has been widely used in various problems of economical statistics, beginning with the work of W. Pareto (1882) on the distribution of profits. It is sometimes accepted that the Pareto distribution describes fairly well the distribution of profits exceeding a certain level in the sense that it must have a tail of order <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p071/p071580/p07158014.png" /> as <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p071/p071580/p07158015.png" />.
−
as $  x \rightarrow \infty $.
 
  
 
====References====
 
====References====
 
<table><TR><TD valign="top">[1]</TD> <TD valign="top">  H. Cramér,  "Mathematical methods of statistics" , Princeton Univ. Press  (1946)</TD></TR></table>
 
<table><TR><TD valign="top">[1]</TD> <TD valign="top">  H. Cramér,  "Mathematical methods of statistics" , Princeton Univ. Press  (1946)</TD></TR></table>
 +
 +
  
 
====Comments====
 
====Comments====
 +
  
 
====References====
 
====References====
 
<table><TR><TD valign="top">[a1]</TD> <TD valign="top">  N.L. Johnson,  S. Kotz,  "Distributions in statistics: continuous univariate distributions" , Houghton Mifflin  (1970)</TD></TR><TR><TD valign="top">[a2]</TD> <TD valign="top">  H.T. Davis,  "Elements of statistics with application to economic data" , Amer. Math. Soc.  (1972)</TD></TR></table>
 
<table><TR><TD valign="top">[a1]</TD> <TD valign="top">  N.L. Johnson,  S. Kotz,  "Distributions in statistics: continuous univariate distributions" , Houghton Mifflin  (1970)</TD></TR><TR><TD valign="top">[a2]</TD> <TD valign="top">  H.T. Davis,  "Elements of statistics with application to economic data" , Amer. Math. Soc.  (1972)</TD></TR></table>

Revision as of 14:52, 7 June 2020

A continuous probability distribution with density

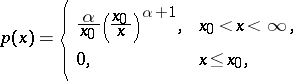depending on two parameters and 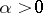. As a "cut-off" version the Pareto distribution can be considered as belonging to the family of beta-distributions (cf. Beta-distribution) of the second kind with the density

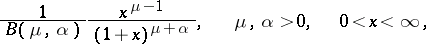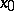for . For any fixed , the Pareto distribution reduces by the transformation to a beta-distribution of the first kind. In the system of Pearson curves the Pareto distribution belongs to those of "type VI" and "type XI" . The mathematical expectation of the Pareto distribution is finite for and equal to 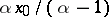; the variance is finite for and equal to 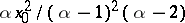; the median is . The Pareto distribution function is defined by the formula

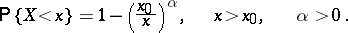The Pareto distribution has been widely used in various problems of economical statistics, beginning with the work of W. Pareto (1882) on the distribution of profits. It is sometimes accepted that the Pareto distribution describes fairly well the distribution of profits exceeding a certain level in the sense that it must have a tail of order 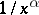as .

References

[1] H. Cramér, "Mathematical methods of statistics" , Princeton Univ. Press (1946)


Comments

References

[a1] N.L. Johnson, S. Kotz, "Distributions in statistics: continuous univariate distributions" , Houghton Mifflin (1970)
[a2] H.T. Davis, "Elements of statistics with application to economic data" , Amer. Math. Soc. (1972)
How to Cite This Entry:
Pareto distribution. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Pareto_distribution&oldid=48130
This article was adapted from an original article by A.V. Prokhorov (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098. See original article
Retrieved from "https://encyclopediaofmath.org/index.php?title=Pareto_distribution&oldid=49356"