Difference between revisions of "Multiplicative ergodic theorem"
Ulf Rehmann (talk | contribs) m (tex encoded by computer) |
Ulf Rehmann (talk | contribs) m (Undo revision 47934 by Ulf Rehmann (talk)) Tag: Undo |
||
| Line 1: | Line 1: | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
''Oseledets's multiplicative ergodic theorem, Oseledec's multiplicative ergodic theorem'' | ''Oseledets's multiplicative ergodic theorem, Oseledec's multiplicative ergodic theorem'' | ||
Consider a linear homogeneous system of differential equations | Consider a linear homogeneous system of differential equations | ||
| − | + | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m065/m065440/m0654401.png" /></td> <td valign="top" style="width:5%;text-align:right;">(a1)</td></tr></table> | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | The Lyapunov exponent of a solution | + | The Lyapunov exponent of a solution <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m065/m065440/m0654402.png" /> of (a1) is defined as |
| − | of (a1) is defined as | ||
| − | + | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m065/m065440/m0654403.png" /></td> </tr></table> | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | A more general setting (Lyapunov exponents for families of system of differential equations) for discussing Lyapunov exponents and related matters is as follows. Let | + | A more general setting (Lyapunov exponents for families of system of differential equations) for discussing Lyapunov exponents and related matters is as follows. Let <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m065/m065440/m0654404.png" /> be a [[Measurable flow|measurable flow]] on a measure space <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m065/m065440/m0654405.png" />. For all <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m065/m065440/m0654406.png" />, let <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m065/m065440/m0654407.png" /> be an <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m065/m065440/m0654408.png" />-dimensional vector space. (Think, for example, of a vector bundle <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m065/m065440/m0654409.png" />.) A cocycle <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m065/m065440/m06544010.png" /> associated with the flow <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m065/m065440/m06544011.png" /> is a measurable function on <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m065/m065440/m06544012.png" /> that assigns to <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m065/m065440/m06544013.png" /> an invertible linear mapping <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m065/m065440/m06544014.png" /> such that |
| − | be a [[Measurable flow|measurable flow]] on a measure space | ||
| − | For all | ||
| − | let | ||
| − | be an | ||
| − | dimensional vector space. (Think, for example, of a vector bundle | ||
| − | A cocycle | ||
| − | associated with the flow | ||
| − | is a measurable function on | ||
| − | that assigns to | ||
| − | an invertible linear mapping | ||
| − | such that | ||
| − | + | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m065/m065440/m06544015.png" /></td> <td valign="top" style="width:5%;text-align:right;">(a2)</td></tr></table> | |
| − | |||
| − | |||
| − | I.e. if the collection of vector spaces | + | I.e. if the collection of vector spaces <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m065/m065440/m06544016.png" /> is viewed as an <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m065/m065440/m06544017.png" />-dimensional vector bundle over <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m065/m065440/m06544018.png" />, then <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m065/m065440/m06544019.png" /> defines an isomorphism of vector bundles <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m065/m065440/m06544020.png" /> over <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m065/m065440/m06544021.png" />, |
| − | is viewed as an | ||
| − | dimensional vector bundle over | ||
| − | then | ||
| − | defines an isomorphism of vector bundles | ||
| − | over | ||
| − | + | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m065/m065440/m06544022.png" /></td> </tr></table> | |
| − | and condition (a2) simply says that | + | and condition (a2) simply says that <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m065/m065440/m06544023.png" />. So <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m065/m065440/m06544024.png" /> is a flow on <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m065/m065440/m06544025.png" /> that lifts <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m065/m065440/m06544026.png" />. <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m065/m065440/m06544027.png" /> is sometimes called the skew product flow defined by <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m065/m065440/m06544028.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m065/m065440/m06544029.png" />. This set-up is sufficiently general to discuss Lyapunov exponents for non-linear flows, and even stochastic non-linear flows and such things as products of random matrices. If <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m065/m065440/m06544030.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m065/m065440/m06544031.png" />, the classical situation (a1) reappears. Let <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m065/m065440/m06544032.png" /> be a differential equation on a manifold <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m065/m065440/m06544033.png" />. Take <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m065/m065440/m06544034.png" />, the tangent bundle over <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m065/m065440/m06544035.png" />. Let <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m065/m065440/m06544036.png" /> be the flow on <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m065/m065440/m06544037.png" /> defined by <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m065/m065440/m06544038.png" />. The associated cocycle is defined by the differential <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m065/m065440/m06544039.png" /> of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m065/m065440/m06544040.png" />, |
| − | So | ||
| − | is a flow on | ||
| − | that lifts | ||
| − | |||
| − | is sometimes called the skew product flow defined by | ||
| − | and | ||
| − | This set-up is sufficiently general to discuss Lyapunov exponents for non-linear flows, and even stochastic non-linear flows and such things as products of random matrices. If | ||
| − | |||
| − | the classical situation (a1) reappears. Let | ||
| − | be a differential equation on a manifold | ||
| − | Take | ||
| − | the tangent bundle over | ||
| − | Let | ||
| − | be the flow on | ||
| − | defined by | ||
| − | The associated cocycle is defined by the differential | ||
| − | of | ||
| − | + | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m065/m065440/m06544041.png" /></td> </tr></table> | |
| − | |||
| − | |||
| − | |||
| − | For a skew product flow | + | For a skew product flow <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m065/m065440/m06544042.png" /> on <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m065/m065440/m06544043.png" /> the Lyapunov exponent at <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m065/m065440/m06544044.png" /> in the direction <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m065/m065440/m06544045.png" /> is defined by |
| − | on | ||
| − | the Lyapunov exponent at | ||
| − | in the direction | ||
| − | is defined by | ||
| − | + | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m065/m065440/m06544046.png" /></td> </tr></table> | |
| − | |||
| − | |||
| − | |||
| − | The multiplicative ergodic theorem of V.I. Oseledets [[#References|[a1]]] now is as follows. Let | + | The multiplicative ergodic theorem of V.I. Oseledets [[#References|[a1]]] now is as follows. Let <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m065/m065440/m06544047.png" /> be a skew product flow and assume that there is an invariant probability measure <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m065/m065440/m06544048.png" /> on <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m065/m065440/m06544049.png" /> for <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m065/m065440/m06544050.png" />, i.e. <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m065/m065440/m06544051.png" /> for all <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m065/m065440/m06544052.png" />. Suppose, moreover, that |
| − | be a skew product flow and assume that there is an invariant probability measure | ||
| − | on | ||
| − | for | ||
| − | i.e. | ||
| − | for all | ||
| − | Suppose, moreover, that | ||
| − | + | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m065/m065440/m06544053.png" /></td> </tr></table> | |
| − | |||
| − | |||
| − | |||
| − | Then there exists a measurable | + | Then there exists a measurable <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m065/m065440/m06544054.png" />-invariant set <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m065/m065440/m06544055.png" /> of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m065/m065440/m06544056.png" />-measure 1 such that for all <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m065/m065440/m06544057.png" /> there are <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m065/m065440/m06544058.png" /> numbers <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m065/m065440/m06544059.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m065/m065440/m06544060.png" />, and corresponding subspaces <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m065/m065440/m06544061.png" /> of dimensions <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m065/m065440/m06544062.png" /> such that for all <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m065/m065440/m06544063.png" />, |
| − | invariant set | ||
| − | of | ||
| − | measure 1 such that for all | ||
| − | there are | ||
| − | numbers | ||
| − | |||
| − | and corresponding subspaces | ||
| − | of dimensions | ||
| − | such that for all | ||
| − | + | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m065/m065440/m06544064.png" /></td> </tr></table> | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | If moreover | + | If moreover <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m065/m065440/m06544065.png" /> is ergodic for <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m065/m065440/m06544066.png" />, i.e. all <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m065/m065440/m06544067.png" />-invariant subsets have <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m065/m065440/m06544068.png" />-measure <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m065/m065440/m06544069.png" /> or <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m065/m065440/m06544070.png" />, then the <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m065/m065440/m06544071.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m065/m065440/m06544072.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m065/m065440/m06544073.png" /> are constants independent of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m065/m065440/m06544074.png" /> (or <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m065/m065440/m06544075.png" />). However, the spaces <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m065/m065440/m06544076.png" /> may still depend on <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m065/m065440/m06544077.png" /> (if the bundle <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m065/m065440/m06544078.png" /> is a trivial bundle so that all the <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m065/m065440/m06544079.png" /> can be identified). The set <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m065/m065440/m06544080.png" /> is called the Lyapunov spectrum of the flow. For more details and applications cf. [[#References|[a2]]], [[#References|[a3]]]. |
| − | is ergodic for | ||
| − | i.e. all | ||
| − | invariant subsets have | ||
| − | measure | ||
| − | or | ||
| − | then the | ||
| − | |||
| − | |||
| − | are constants independent of | ||
| − | or | ||
| − | However, the spaces | ||
| − | may still depend on | ||
| − | if the bundle | ||
| − | is a trivial bundle so that all the | ||
| − | can be identified). The set | ||
| − | is called the Lyapunov spectrum of the flow. For more details and applications cf. [[#References|[a2]]], [[#References|[a3]]]. | ||
====References==== | ====References==== | ||
<table><TR><TD valign="top">[a1]</TD> <TD valign="top"> V.I. [V.I. Oseledets] Oseledec, "A multiplicative ergodic theorem. Lyapunov characteristic numbers for dynamical systems" ''Trans. Moscow Math. Soc.'' , '''19''' (1968) pp. 197–231 ''Trudy Moskov. Mat. Obshch.'' , '''19''' (1968) pp. 179–210</TD></TR><TR><TD valign="top">[a2]</TD> <TD valign="top"> W. Kliemann, "Analysis of nonlinear stochastic systems" W. Schiehlen (ed.) W. Wedig (ed.) , ''Analysis and estimation of stochastic mechanical systems'' , Springer (Wien) (1988) pp. 43–102</TD></TR><TR><TD valign="top">[a3]</TD> <TD valign="top"> L. Arnold (ed.) V. Wihstutz (ed.) , ''Lyapunov exponents'' , ''Lect. notes in math.'' , '''1186''' , Springer (1986)</TD></TR></table> | <table><TR><TD valign="top">[a1]</TD> <TD valign="top"> V.I. [V.I. Oseledets] Oseledec, "A multiplicative ergodic theorem. Lyapunov characteristic numbers for dynamical systems" ''Trans. Moscow Math. Soc.'' , '''19''' (1968) pp. 197–231 ''Trudy Moskov. Mat. Obshch.'' , '''19''' (1968) pp. 179–210</TD></TR><TR><TD valign="top">[a2]</TD> <TD valign="top"> W. Kliemann, "Analysis of nonlinear stochastic systems" W. Schiehlen (ed.) W. Wedig (ed.) , ''Analysis and estimation of stochastic mechanical systems'' , Springer (Wien) (1988) pp. 43–102</TD></TR><TR><TD valign="top">[a3]</TD> <TD valign="top"> L. Arnold (ed.) V. Wihstutz (ed.) , ''Lyapunov exponents'' , ''Lect. notes in math.'' , '''1186''' , Springer (1986)</TD></TR></table> | ||
Revision as of 14:32, 7 June 2020
Oseledets's multiplicative ergodic theorem, Oseledec's multiplicative ergodic theorem
Consider a linear homogeneous system of differential equations
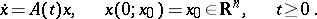 | (a1) |
The Lyapunov exponent of a solution  of (a1) is defined as
of (a1) is defined as
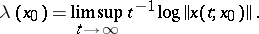 |
A more general setting (Lyapunov exponents for families of system of differential equations) for discussing Lyapunov exponents and related matters is as follows. Let  be a measurable flow on a measure space
be a measurable flow on a measure space 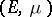 . For all
. For all 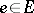 , let
, let 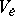 be an
be an  -dimensional vector space. (Think, for example, of a vector bundle
-dimensional vector space. (Think, for example, of a vector bundle 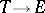 .) A cocycle
.) A cocycle  associated with the flow
associated with the flow 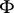 is a measurable function on
is a measurable function on 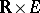 that assigns to
that assigns to 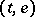 an invertible linear mapping
an invertible linear mapping 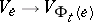 such that
such that
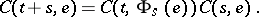 | (a2) |
I.e. if the collection of vector spaces 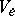 is viewed as an
is viewed as an  -dimensional vector bundle over
-dimensional vector bundle over 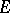 , then
, then 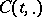 defines an isomorphism of vector bundles
defines an isomorphism of vector bundles 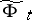 over
over 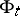 ,
,
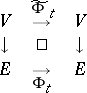 |
and condition (a2) simply says that 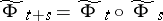 . So
. So 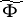 is a flow on
is a flow on  that lifts
that lifts 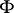 .
. 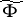 is sometimes called the skew product flow defined by
is sometimes called the skew product flow defined by 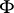 and
and 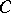 . This set-up is sufficiently general to discuss Lyapunov exponents for non-linear flows, and even stochastic non-linear flows and such things as products of random matrices. If
. This set-up is sufficiently general to discuss Lyapunov exponents for non-linear flows, and even stochastic non-linear flows and such things as products of random matrices. If 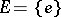 ,
,  , the classical situation (a1) reappears. Let
, the classical situation (a1) reappears. Let 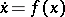 be a differential equation on a manifold
be a differential equation on a manifold 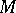 . Take
. Take 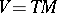 , the tangent bundle over
, the tangent bundle over 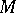 . Let
. Let 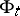 be the flow on
be the flow on 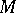 defined by
defined by 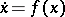 . The associated cocycle is defined by the differential
. The associated cocycle is defined by the differential  of
of 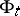 ,
,
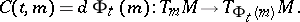 |
For a skew product flow 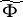 on
on 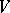 the Lyapunov exponent at
the Lyapunov exponent at 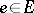 in the direction
in the direction  is defined by
is defined by
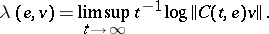 |
The multiplicative ergodic theorem of V.I. Oseledets [a1] now is as follows. Let 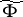 be a skew product flow and assume that there is an invariant probability measure
be a skew product flow and assume that there is an invariant probability measure 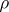 on
on 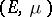 for
for 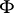 , i.e.
, i.e. 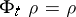 for all
for all 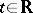 . Suppose, moreover, that
. Suppose, moreover, that
 |
Then there exists a measurable 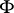 -invariant set
-invariant set 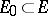 of
of 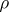 -measure 1 such that for all
-measure 1 such that for all 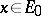 there are
there are 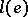 numbers
numbers 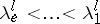 ,
, 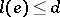 , and corresponding subspaces
, and corresponding subspaces 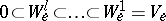 of dimensions
of dimensions 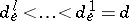 such that for all
such that for all 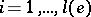 ,
,
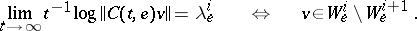 |
If moreover 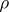 is ergodic for
is ergodic for 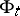 , i.e. all
, i.e. all 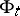 -invariant subsets have
-invariant subsets have 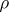 -measure
-measure  or
or 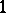 , then the
, then the 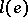 ,
, 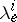 ,
, 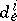 are constants independent of
are constants independent of  (or
(or 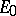 ). However, the spaces
). However, the spaces 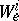 may still depend on
may still depend on 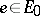 (if the bundle
(if the bundle 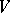 is a trivial bundle so that all the
is a trivial bundle so that all the 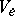 can be identified). The set
can be identified). The set 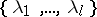 is called the Lyapunov spectrum of the flow. For more details and applications cf. [a2], [a3].
is called the Lyapunov spectrum of the flow. For more details and applications cf. [a2], [a3].
References
| [a1] | V.I. [V.I. Oseledets] Oseledec, "A multiplicative ergodic theorem. Lyapunov characteristic numbers for dynamical systems" Trans. Moscow Math. Soc. , 19 (1968) pp. 197–231 Trudy Moskov. Mat. Obshch. , 19 (1968) pp. 179–210 |
| [a2] | W. Kliemann, "Analysis of nonlinear stochastic systems" W. Schiehlen (ed.) W. Wedig (ed.) , Analysis and estimation of stochastic mechanical systems , Springer (Wien) (1988) pp. 43–102 |
| [a3] | L. Arnold (ed.) V. Wihstutz (ed.) , Lyapunov exponents , Lect. notes in math. , 1186 , Springer (1986) |
Multiplicative ergodic theorem. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Multiplicative_ergodic_theorem&oldid=47934