Difference between revisions of "User:Maximilian Janisch/Sandbox"
(copy of bayesian approach) |
m (typo) |
||
| Line 1: | Line 1: | ||
<div class="Vorlage_Achtung" style="border: 0.18em solid #FF6666; border-left:1em solid #FF6666; margin:0.5em 0em; overflow:hidden; padding:0.5em; text-align: left;"> | <div class="Vorlage_Achtung" style="border: 0.18em solid #FF6666; border-left:1em solid #FF6666; margin:0.5em 0em; overflow:hidden; padding:0.5em; text-align: left;"> | ||
| − | This page is copy of the article [[Bayesian approach]] in order to test [[User:Maximilian_Janisch/latexlist|automatic LaTeXification]]. This article is not my work. | + | This page is a copy of the article [[Bayesian approach]] in order to test [[User:Maximilian_Janisch/latexlist|automatic LaTeXification]]. This article is not my work. |
</div> | </div> | ||
Revision as of 09:31, 1 September 2019
to statistical problems
An approach based on the assumption that to any parameter in a statistical problem there can be assigned a definite probability distribution. Any general statistical decision problem is determined by the following elements: by a space  of (potential) samples
of (potential) samples  , by a space
, by a space  of values of the unknown parameter
of values of the unknown parameter  , by a family of probability distributions
, by a family of probability distributions  on
on  , by a space of decisions
, by a space of decisions  and by a function
and by a function 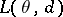 , which characterizes the losses caused by accepting the decision
, which characterizes the losses caused by accepting the decision  when the true value of the parameter is
when the true value of the parameter is  . The objective of decision making is to find in a certain sense an optimal rule (decision function)
. The objective of decision making is to find in a certain sense an optimal rule (decision function) 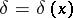 , assigning to each result of an observation
, assigning to each result of an observation 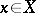 the decision
the decision 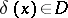 . In the Bayesian approach, when it is assumed that the unknown parameter
. In the Bayesian approach, when it is assumed that the unknown parameter 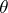 is a random variable with a given (a priori) distribution
is a random variable with a given (a priori) distribution 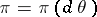 on
on 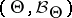 the best decision function (Bayesian decision function)
the best decision function (Bayesian decision function) 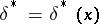 is defined as the function for which the minimum expected loss
is defined as the function for which the minimum expected loss 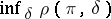 , where
, where
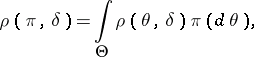 |
and
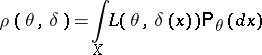 |
is attained. Thus,
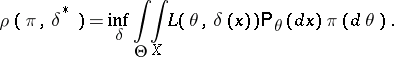 |
In searching for the Bayesian decision function 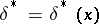 , the following remark is useful. Let
, the following remark is useful. Let 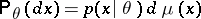 ,
, 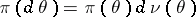 , where
, where 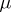 and
and  are certain
are certain 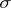 -finite measures. One then finds, assuming that the order of integration may be changed,
-finite measures. One then finds, assuming that the order of integration may be changed,
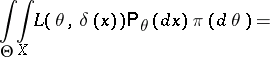 |
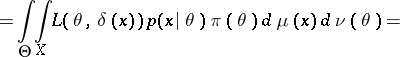 |
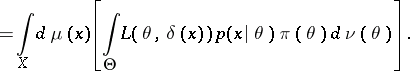 |
It is seen from the above that for a given 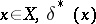 is that value of
is that value of 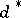 for which
for which
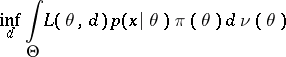 |
is attained, or, what is equivalent, for which
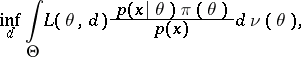 |
is attained, where
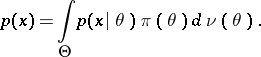 |
But, according to the Bayes formula
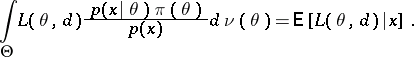 |
Thus, for a given  ,
, 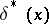 is that value of
is that value of  for which the conditional average loss
for which the conditional average loss  attains a minimum.
attains a minimum.
Example. (The Bayesian approach applied to the case of distinguishing between two simple hypotheses.) Let 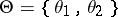 ,
, 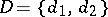 ,
, 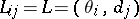 ,
, 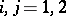 ;
;  ,
, 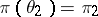 ,
, 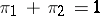 . If the solution
. If the solution 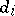 is identified with the acceptance of the hypothesis
is identified with the acceptance of the hypothesis 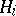 :
: 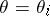 , it is natural to assume that
, it is natural to assume that 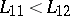 ,
, 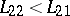 . Then
. Then
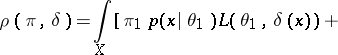 |
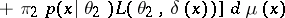 |
implies that  is attained for the function
is attained for the function
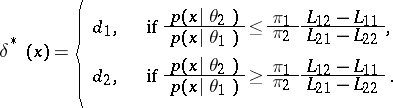 |
The advantage of the Bayesian approach consists in the fact that, unlike the losses 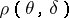 , the expected losses
, the expected losses  are numbers which are dependent on the unknown parameter
are numbers which are dependent on the unknown parameter  , and, consequently, it is known that solutions
, and, consequently, it is known that solutions 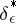 for which
for which
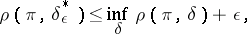 |
and which are, if not optimal, at least  -optimal
-optimal 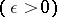 , are certain to exist. The disadvantage of the Bayesian approach is the necessity of postulating both the existence of an a priori distribution of the unknown parameter and its precise form (the latter disadvantage may be overcome to a certain extent by adopting an empirical Bayesian approach, cf. Bayesian approach, empirical).
, are certain to exist. The disadvantage of the Bayesian approach is the necessity of postulating both the existence of an a priori distribution of the unknown parameter and its precise form (the latter disadvantage may be overcome to a certain extent by adopting an empirical Bayesian approach, cf. Bayesian approach, empirical).
References
| [1] | A. Wald, "Statistical decision functions" , Wiley (1950) |
| [2] | M.H. de Groot, "Optimal statistical decisions" , McGraw-Hill (1970) |
Maximilian Janisch/Sandbox. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Maximilian_Janisch/Sandbox&oldid=43804