Difference between revisions of "Talk:Elementary matrix"
Neo razgriz (talk | contribs) (Added a note to the (example) alternative definition.) |
Neo razgriz (talk | contribs) m |
||
| Line 19: | Line 19: | ||
In mathematics, an '''elementary matrix''' is a matrix which differs from the identity matrix by one single elementary row operation.<ref name="wiki2">[http://en.wikipedia.org/wiki/Elementary_matrix Wikipedia - Elementary matrix]</ref> | In mathematics, an '''elementary matrix''' is a matrix which differs from the identity matrix by one single elementary row operation.<ref name="wiki2">[http://en.wikipedia.org/wiki/Elementary_matrix Wikipedia - Elementary matrix]</ref> | ||
| − | Although | + | Although this definition requires '''elementary row operations''' to be defined, the matrix that matches the Row-switch operation is "elementary", by this definition. |
== References == | == References == | ||
| Line 32: | Line 32: | ||
:: Theorems regarding the connection between elementary row operations and elementary matrices are based on this definition. | :: Theorems regarding the connection between elementary row operations and elementary matrices are based on this definition. | ||
| − | :: Pending review by an Algebraist. --[[User:Neo_razgriz|Ben Paradise]] ([[ | + | :: Pending review by an Algebraist. --[[User:Neo_razgriz|Ben Paradise]] ([[User talk:Neo_razgriz|talk]]) 19:49, 20 March 2015 (CET) |
Revision as of 21:05, 20 March 2015
Issue
This definition excludes the row-switching elementary matrix[1]:
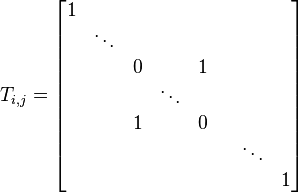
Proof
The matrix above (marked T) has more than one off-diagonal element added to it.
In addition, at least one diagonal element has been modified.
Therefore, by the definition on the Elementary matrix page, T is not an elementary matrix.
Alternative definition (example)
Wikipedia defines elementary matrix in the following manner:
In mathematics, an elementary matrix is a matrix which differs from the identity matrix by one single elementary row operation.[2]
Although this definition requires elementary row operations to be defined, the matrix that matches the Row-switch operation is "elementary", by this definition.
References
--Ben Paradise (talk) 14:24, 20 March 2015 (CET)
- Thank you. Probably you are right. But, being not an algebraist, I am not sure: maybe different (non-equivalent) definitions are in use? Boris Tsirelson (talk) 19:13, 20 March 2015 (CET)
- Thanks for the reply. I also noticed that the same issue exists for Row-multiplying transformations.
- Theorems regarding the connection between elementary row operations and elementary matrices are based on this definition.
- Pending review by an Algebraist. --Ben Paradise (talk) 19:49, 20 March 2015 (CET)
Elementary matrix. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Elementary_matrix&oldid=36337