Difference between revisions of "Absolutely convergent series"
| Line 7: | Line 7: | ||
\sum_{i=0}^\infty |a_n| | \sum_{i=0}^\infty |a_n| | ||
\end{equation} | \end{equation} | ||
| − | converges (in the case of a general Banach space the series | + | converges (in the case of a general Banach space the series \ref{e:serie_norme} must be |
substituted by $\sum \|a_n\|_A$, where $\|\cdot\|_A$ denotes the norm in $A$). | substituted by $\sum \|a_n\|_A$, where $\|\cdot\|_A$ denotes the norm in $A$). | ||
| + | The absolute convergence implies the convergence. However the opposite is false, | ||
| + | see for instance | ||
| + | \[ | ||
| + | \sum_{n=0}^\infty (-1)^n \frac{1}{n+1}\, . | ||
| + | \] | ||
| − | + | For a series to converge absolutely, a necessary and sufficient condition (Cauchy's criterion for the absolute convergence of a series) is that for any <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/a/a010/a010390/a0103903.png" /> there exist a number <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/a/a010/a010390/a0103904.png" /> such that for all numbers <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/a/a010/a010390/a0103905.png" /> and for all integers <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/a/a010/a010390/a0103906.png" /> the inequality | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | For a series | ||
<table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/a/a010/a010390/a0103907.png" /></td> </tr></table> | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/a/a010/a010390/a0103907.png" /></td> </tr></table> | ||
Revision as of 16:58, 20 July 2012
A series of real or complex numbers, or more in general of elements in a Banach space $A$, \begin{equation}\label{e:serie} \sum_{i=0}^\infty a_n \end{equation} for which the series of real numbers \begin{equation}\label{e:serie_norme} \sum_{i=0}^\infty |a_n| \end{equation} converges (in the case of a general Banach space the series \ref{e:serie_norme} must be substituted by $\sum \|a_n\|_A$, where $\|\cdot\|_A$ denotes the norm in $A$). The absolute convergence implies the convergence. However the opposite is false, see for instance \[ \sum_{n=0}^\infty (-1)^n \frac{1}{n+1}\, . \]
For a series to converge absolutely, a necessary and sufficient condition (Cauchy's criterion for the absolute convergence of a series) is that for any 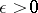 there exist a number
there exist a number 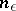 such that for all numbers
such that for all numbers 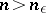 and for all integers
and for all integers 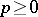 the inequality
the inequality
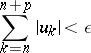 |
is true. If a series is absolutely convergent, it is also convergent. The series
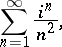 |
where 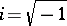 , is absolutely convergent; the series
, is absolutely convergent; the series
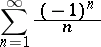 |
is convergent, but not absolutely convergent. Let
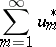 | (3) |
be a series consisting of the same terms as the series (1) but taken, in general, in a different order. Since the series (1) is absolutely convergent, so is the series (3), and the sum of the series (3) is equal to the sum of the series (1). If the series
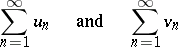 |
are both absolutely convergent, so is any one of their linear combinations
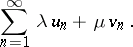 |
The series of all possible pairwise products 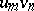 of the terms of these series, arranged in an arbitrary order, is also absolutely convergent, and its sum is equal to the product of the sums of the original series. These properties of absolutely-convergent series are also displayed by multiple series:
of the terms of these series, arranged in an arbitrary order, is also absolutely convergent, and its sum is equal to the product of the sums of the original series. These properties of absolutely-convergent series are also displayed by multiple series:
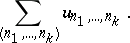 | (4) |
If a multiple series is absolutely convergent, it is convergent, for example, both in the sense of spherical and of rectangular partial sums, and its sums will be the same in both cases. If the multiple series (4) is absolutely convergent, the iterated series
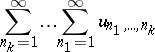 | (5) |
is absolutely convergent, i.e. all series obtained by successive summation of terms of the series (4) by the indices  are absolutely convergent; moreover, the sums of the multiple series (4) and the iterated series (5) are identical with the sum of any simple series formed by all terms of the series (4).
are absolutely convergent; moreover, the sums of the multiple series (4) and the iterated series (5) are identical with the sum of any simple series formed by all terms of the series (4).
If the terms of the series (1) are elements of some Banach space with norm 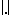 , the series (1) is said to be absolutely convergent if the series
, the series (1) is said to be absolutely convergent if the series
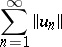 |
is absolutely convergent. The properties of absolutely-convergent series of numbers discussed above can also be generalized to include the case of absolutely-convergent series of elements of a Banach space. In particular, (the partial sums of) an absolutely-convergent series in a Banach space converge(s) in that space. The concept of an absolutely-convergent series is applied in a similar manner to multiple series in a Banach space.
References
| [1] | V.A. Il'in, E.G. Poznyak, "Fundamentals of mathematical analysis" , 1–2 , MIR (1982) (Translated from Russian) |
| [2] | L.D. Kudryavtsev, "Mathematical analysis" , 1 , Moscow (1973) (In Russian) |
| [3] | S.M. Nikol'skii, "A course of mathematical analysis" , 1 , MIR (1977) (Translated from Russian) |
Comments
A useful Western reference is [a1].
References
| [a1] | T.M. Apostol, "Mathematical analysis" , Addison-Wesley (1969) |
Absolutely convergent series. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Absolutely_convergent_series&oldid=27095