Difference between revisions of "Lattice distribution"
(→References: Feller: internal link) |
(→References: Gnedenko: internal link) |
||
| Line 24: | Line 24: | ||
====References==== | ====References==== | ||
| − | <table><TR><TD valign="top">[1]</TD> <TD valign="top"> B.V. Gnedenko, "The theory of probability" , Chelsea, reprint (1962) (Translated from Russian)</TD></TR><TR><TD valign="top">[2]</TD> <TD valign="top"> V.V. Petrov, "Sums of independent random variables" , Springer (1975) (Translated from Russian)</TD></TR><TR><TD valign="top">[3]</TD> <TD valign="top"> Yu.V. [Yu.V. Prokhorov] Prohorov, Yu.A. Rozanov, "Probability theory, basic concepts. Limit theorems, random processes" , Springer (1969) (Translated from Russian)</TD></TR></table> | + | <table><TR><TD valign="top">[1]</TD> <TD valign="top"> B.V. Gnedenko, [[Gnedenko, "A course in the theory of probability"|"The theory of probability"]], Chelsea, reprint (1962) (Translated from Russian)</TD></TR> |
| − | + | <TR><TD valign="top">[2]</TD> <TD valign="top"> V.V. Petrov, "Sums of independent random variables" , Springer (1975) (Translated from Russian)</TD></TR><TR><TD valign="top">[3]</TD> <TD valign="top"> Yu.V. [Yu.V. Prokhorov] Prohorov, Yu.A. Rozanov, "Probability theory, basic concepts. Limit theorems, random processes" , Springer (1969) (Translated from Russian)</TD></TR></table> | |
| − | |||
====Comments==== | ====Comments==== | ||
Revision as of 12:08, 1 May 2012
A discrete probability distribution concentrated on a set of points of the form 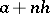 , where
, where 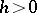 ,
,  is a real number and
is a real number and 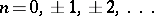 . The number
. The number 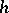 is called the step of the lattice distribution, and if for no
is called the step of the lattice distribution, and if for no 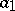 and
and 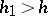 the distribution is concentrated on a set of the form
the distribution is concentrated on a set of the form 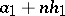 ,
, 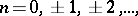 then
then 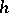 is called the maximal step. An arithmetic distribution is a particular case (
is called the maximal step. An arithmetic distribution is a particular case (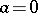 ) of a lattice distribution.
) of a lattice distribution.
For a probability distribution with characteristic function 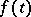 to be a lattice distribution it is necessary and sufficient that there exists a real number
to be a lattice distribution it is necessary and sufficient that there exists a real number 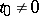 such that
such that 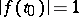 ; in this case
; in this case 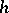 is the maximal step if and only if
is the maximal step if and only if 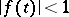 for
for 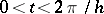 and
and 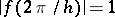 . The characteristic function of a lattice distribution is periodic.
. The characteristic function of a lattice distribution is periodic.
The inversion formula for a lattice distribution has the form
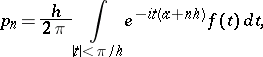 |
where 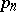 is the probability that the lattice distribution ascribes to the point
is the probability that the lattice distribution ascribes to the point 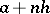 and
and 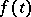 is the corresponding characteristic function. The following equality also holds:
is the corresponding characteristic function. The following equality also holds:
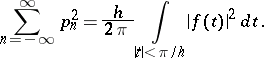 |
The convolution of two lattice distributions with steps 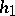 and
and 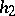 and with finite supports is a lattice distribution if and only if
and with finite supports is a lattice distribution if and only if 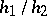 is a rational number.
is a rational number.
In the study of the limit behaviour of sums of independent random variables, the basic result of the central limit theorem on convergence towards the normal distribution is considerably complemented by local theorems for lattice distributions. The simplest example of a local theorem for lattice distributions is the Laplace theorem, which can be generalized as follows: Let 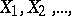 be a sequence of independent identically-distributed random variables with
be a sequence of independent identically-distributed random variables with 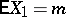 ,
, 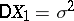 , and let
, and let 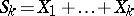 while
while 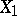 takes values of the form
takes values of the form  ,
, 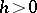 . Put
. Put
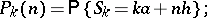 |
for the asymptotic relation
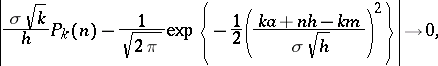 |
as 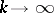 , to be true uniformly with respect to
, to be true uniformly with respect to  , it is necessary and sufficient that the step
, it is necessary and sufficient that the step 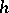 is the maximal step.
is the maximal step.
References
| [1] | B.V. Gnedenko, "The theory of probability", Chelsea, reprint (1962) (Translated from Russian) |
| [2] | V.V. Petrov, "Sums of independent random variables" , Springer (1975) (Translated from Russian) |
| [3] | Yu.V. [Yu.V. Prokhorov] Prohorov, Yu.A. Rozanov, "Probability theory, basic concepts. Limit theorems, random processes" , Springer (1969) (Translated from Russian) |
Comments
References
| [a1] | W. Feller, "An introduction to probability theory and its applications", 1–2 , Wiley (1957–1971) |
| [a2] | E. Lukacs, "Characteristic functions" , Griffin (1970) |
| [a3] | N.L. Johnson, S. Kotz, "Distributions in statistics: discrete distributions" , Mifflin (1969) |
Lattice distribution. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Lattice_distribution&oldid=25523