Difference between revisions of "Hölder space"
From Encyclopedia of Mathematics
Ulf Rehmann (talk | contribs) m (moved Holder space to Hölder space over redirect: accented title) |
(ball, not sphere (translation error, probably)) |
||
| Line 19: | Line 19: | ||
1) <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/h/h047/h047516/h04751627.png" /> is imbedded in <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/h/h047/h047516/h04751628.png" /> if <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/h/h047/h047516/h04751629.png" />, where <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/h/h047/h047516/h04751630.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/h/h047/h047516/h04751631.png" /> are integers, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/h/h047/h047516/h04751632.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/h/h047/h047516/h04751633.png" />. Here <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/h/h047/h047516/h04751634.png" /> and the constant <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/h/h047/h047516/h04751635.png" /> is independent of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/h/h047/h047516/h04751636.png" />. | 1) <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/h/h047/h047516/h04751627.png" /> is imbedded in <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/h/h047/h047516/h04751628.png" /> if <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/h/h047/h047516/h04751629.png" />, where <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/h/h047/h047516/h04751630.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/h/h047/h047516/h04751631.png" /> are integers, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/h/h047/h047516/h04751632.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/h/h047/h047516/h04751633.png" />. Here <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/h/h047/h047516/h04751634.png" /> and the constant <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/h/h047/h047516/h04751635.png" /> is independent of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/h/h047/h047516/h04751636.png" />. | ||
| − | 2) The unit | + | 2) The unit ball of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/h/h047/h047516/h04751637.png" /> is compact in <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/h/h047/h047516/h04751638.png" /> if <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/h/h047/h047516/h04751639.png" />. Consequently, any bounded set of functions from <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/h/h047/h047516/h04751640.png" /> contains a sequence of functions that converges in the metric of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/h/h047/h047516/h04751641.png" /> to a function of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/h/h047/h047516/h04751642.png" />. |
====References==== | ====References==== | ||
Revision as of 11:46, 16 May 2015
A Banach space of bounded continuous functions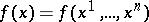 
defined on a set 
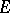of an 
-dimensional Euclidean space and satisfying a Hölder condition on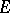 
.
The Hölder space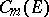 
, where 
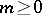is an integer, consists of the functions that are 
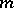times continuously differentiable on 
(continuous for 
).
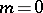The Hölder space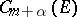 
, 
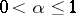, where 
is an integer, consists of the functions that are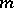 
times continuously differentiable (continuous for 
) and whose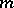 
-th derivatives satisfy the Hölder condition with index 
.
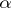For bounded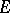 
a norm is introduced in 
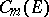and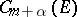 
as follows:
 |
 |
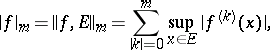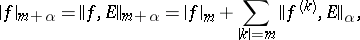where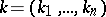 
, 
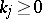is an integer,
 |
The fundamental properties of Hölder spaces for a bounded connected domain (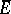
is the closure of 
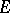) are:
1) 
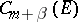is imbedded in 
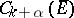if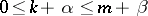 
, where 
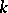and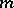 
are integers, 
, 
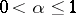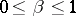. Here 
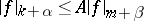and the constant 
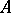is independent of 
.
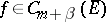2) The unit ball of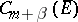 
is compact in 
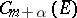if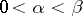 
. Consequently, any bounded set of functions from 
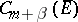contains a sequence of functions that converges in the metric of 
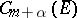to a function of 
.
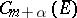References
| [1] | C. Miranda, "Partial differential equations of elliptic type" , Springer (1970) (Translated from Italian) |
Comments
If, in the above,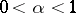 
, then 
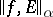is the Hölder 
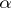-semi-norm of 
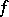on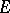 
, i.e.
 |
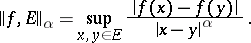See Hölder condition, where this norm is denoted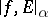 
.
Hölder spaces play a role in partial differential equations, potential theory, complex analysis, functional analysis (cf. Imbedding theorems), etc.
How to Cite This Entry:
Hölder space. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=H%C3%B6lder_space&oldid=23330
Hölder space. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=H%C3%B6lder_space&oldid=23330
This article was adapted from an original article by L.P. Kuptsov (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098. See original article