Difference between revisions of "Schläfli integral"
From Encyclopedia of Mathematics
Ulf Rehmann (talk | contribs) m (moved Schläfli integral to Schlaefli integral: ascii title) |
Ulf Rehmann (talk | contribs) m (moved Schlaefli integral to Schläfli integral over redirect: accented title) |
(No difference)
| |
Revision as of 07:55, 26 March 2012
An integral representation of the Bessel functions for any  :
:
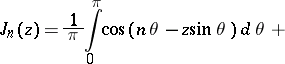 | (*) |
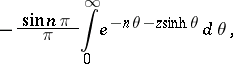 |
when  . It is valid for all integer
. It is valid for all integer  . Formula (*) can be derived from
. Formula (*) can be derived from
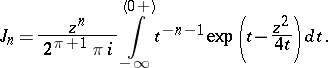 |
Formula (*) was first given by L. Schläfli .
An integral representation of the Legendre polynomials:
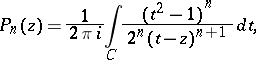 |
where 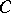 is a contour making one counter-clockwise turn around
is a contour making one counter-clockwise turn around  . This representation was first given by L. Schläfli [2].
. This representation was first given by L. Schläfli [2].
References
| [1] | L. Schläfli, "Eine Bemerkung zu Herrn Neumanns Untersuchungen über die Besselschen Funktionen" Math. Ann. , 3 : 1 (1871) pp. 134–149 |
| [2] | L. Schläfli, "Über die zwei Heine'schen Kugelfunktionen mit beliebigem Parameter und ihre ausnahmslose Darstellung durch bestimmte Integrale" , H. Koerber , Berlin (1881) |
| [3] | E.T. Whittaker, G.N. Watson, "A course of modern analysis" , Cambridge Univ. Press (1952) pp. Chapt. 6 |
| [4] | A. Krazer, W. Franz, "Transzendente Funktionen" , Akademie Verlag (1960) |
Comments
The reduction of the Schläfli integral to the second integral representation for 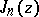 is valid for unrestricted values of
is valid for unrestricted values of  (see also [a3], 6.2
(see also [a3], 6.2
and ). The integral representation for the Legendre polynomials follows from the Rodrigues formula, similarly as for the Jacobi polynomials (cf. [a2], (4.4.6) and (4.8.1)).
References
| [a1] | F.W.J. Olver, "Asymptotics and special functions" , Acad. Press (1974) |
| [a2] | G. Szegö, "Orthogonal polynomials" , Amer. Math. Soc. (1975) |
| [a3] | G.N. Watson, "A treatise on the theory of Bessel functions" , 1 , Cambridge Univ. Press (1952) |
How to Cite This Entry:
Schläfli integral. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Schl%C3%A4fli_integral&oldid=23005
Schläfli integral. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Schl%C3%A4fli_integral&oldid=23005
This article was adapted from an original article by A.B. Ivanov (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098. See original article