Difference between revisions of "Frénet trihedron"
From Encyclopedia of Mathematics
Ulf Rehmann (talk | contribs) m (moved Frénet trihedron to Frenet trihedron: ascii title) |
Ulf Rehmann (talk | contribs) m (moved Frenet trihedron to Frénet trihedron over redirect: accented title) |
(No difference)
| |
Revision as of 07:54, 26 March 2012
natural trihedron
The trihedral angle formed by the rays emanating from a point 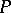 of a regular curve
of a regular curve 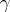 in the respective directions of the tangent
in the respective directions of the tangent  , the normal
, the normal  and the binormal
and the binormal 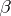 to the curve. If the
to the curve. If the 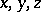 coordinate axes, respectively, lie along the sides of the Frénet trihedron, then the equation of the curve in this coordinate system has the form
coordinate axes, respectively, lie along the sides of the Frénet trihedron, then the equation of the curve in this coordinate system has the form
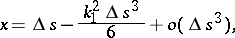 |
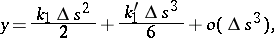 |
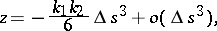 |
where 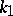 and
and 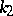 are the curvature and torsion of the curve, and
are the curvature and torsion of the curve, and  is the natural parameter. The qualitative form of the projections of the curve onto the planes of the Frénet trihedron for
is the natural parameter. The qualitative form of the projections of the curve onto the planes of the Frénet trihedron for 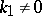 and
and 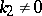 can be seen in the figures.
can be seen in the figures.

Figure: f041700a

Figure: f041700b

Figure: f041700c
This trihedron was studied by F. Frénet (1847).
Comments
References
| [a1] | C.C. Hsiung, "A first course in differential geometry" , Wiley (1981) pp. Chapt. 3, Sect. 4 |
How to Cite This Entry:
Frénet trihedron. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Fr%C3%A9net_trihedron&oldid=22469
Frénet trihedron. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Fr%C3%A9net_trihedron&oldid=22469
This article was adapted from an original article by D.D. Sokolov (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098. See original article