Difference between revisions of "Erdös problem"
Ulf Rehmann (talk | contribs) m (moved Erdös problem to Erdos problem: ascii title) |
Ulf Rehmann (talk | contribs) m (moved Erdos problem to Erdös problem over redirect: accented title) |
(No difference)
| |
Revision as of 07:54, 26 March 2012
The problem on the existence in an  -dimensional Euclidean space
-dimensional Euclidean space 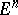 of a set of more than
of a set of more than 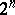 points, any three of which form a non-obtuse triangle (the Erdös property). It was posed by P. Erdös (see [1]), who also made the conjecture (proved in [2]) that the problem has a negative answer and that a set having the Erdös property contains
points, any three of which form a non-obtuse triangle (the Erdös property). It was posed by P. Erdös (see [1]), who also made the conjecture (proved in [2]) that the problem has a negative answer and that a set having the Erdös property contains 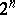 elements if and only if it consists of the set of vertices of a rectangular parallelopipedon in
elements if and only if it consists of the set of vertices of a rectangular parallelopipedon in 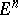 . The proof of this assertion also solved the so-called Klee problem: What is the number of vertices
. The proof of this assertion also solved the so-called Klee problem: What is the number of vertices 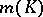 of a polyhedron
of a polyhedron 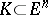 if any two of its vertices lie in distinct parallel supporting hyperplanes of
if any two of its vertices lie in distinct parallel supporting hyperplanes of 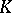 (the Klee property). If a set
(the Klee property). If a set 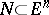 has the Erdös property, then the convex hull
has the Erdös property, then the convex hull  of
of 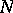 is a polyhedron having the Klee property and
is a polyhedron having the Klee property and  is equal to the cardinality of
is equal to the cardinality of 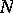 . If a polyhedron
. If a polyhedron 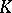 has the Klee property, then
has the Klee property, then 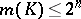 . The equality
. The equality 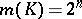 characterizes
characterizes  -dimensional parallelopipeda in the set of all polyhedra having the Klee property.
-dimensional parallelopipeda in the set of all polyhedra having the Klee property.
The Erdös problem is connected with the Hadwiger hypothesis 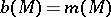 .
.
References
| [1] | P. Erdös, "Some unsolved problems" Michigan J. Math. , 4 (1957) pp. 291–300 |
| [2] | L. Danzer, B. Grünbaum, "Ueber zwei Probleme bezüglich konvexer Körpern von P. Erdös und von V.L. Klee" Math.Z. , 79 (1962) pp. 95–99 |
Comments
This Erdös problem was first stated (for 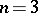 ) in [a1], the Klee problem in [a2].
) in [a1], the Klee problem in [a2].
References
| [a1] | P. Erdös, "Problem 4306" Amer. Math. Monthly , 55 (1948) pp. 431 |
| [a2] | V.L. Klee, "Unsolved problems in intuitive geometry" , Seattle (1960) (Mimeographed notes) |
Erdös problem. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Erd%C3%B6s_problem&oldid=22385