Difference between revisions of "Carathéodory measure"
From Encyclopedia of Mathematics
Ulf Rehmann (talk | contribs) m (moved Carathéodory measure to Caratheodory measure: ascii title) |
Ulf Rehmann (talk | contribs) m (moved Caratheodory measure to Carathéodory measure over redirect: accented title) |
(No difference)
| |
Revision as of 07:54, 26 March 2012
The measure 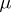 induced by the outer Carathéodory measure
induced by the outer Carathéodory measure 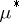 , the latter being an outer measure defined on the class of all subsets of a metric space
, the latter being an outer measure defined on the class of all subsets of a metric space 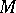 (with a metric
(with a metric 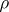 ) such that
) such that
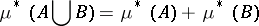 |
if 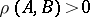 . It was introduced by C. Carathéodory [1]. A set
. It was introduced by C. Carathéodory [1]. A set 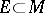 belongs to the domain of definition of
belongs to the domain of definition of 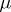 , i.e. is
, i.e. is 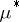 -measurable, if and only if
-measurable, if and only if
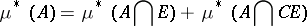 |
for every 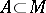 (here
(here 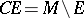 ). If
). If 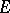 is
is 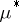 -measurable, then
-measurable, then 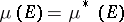 . The domain of definition of a Carathéodory measure contains all Borel sets. If
. The domain of definition of a Carathéodory measure contains all Borel sets. If 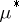 is an outer measure on the class of all subsets of a metric space such that every open set is
is an outer measure on the class of all subsets of a metric space such that every open set is 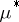 -measurable, then
-measurable, then 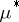 is an outer Carathéodory measure.
is an outer Carathéodory measure.
References
| [1] | C. Carathéodory, "Ueber das lineare Mass von Punktmengen, eine Verallgemeinerung des Längenbegriffs" Nachr. Gesell. Wiss. Göttingen (1914) pp. 404–426 |
| [2] | S. Saks, "Theory of the integral" , Hafner (1952) (Translated from French) |
| [3] | P.R. Halmos, "Measure theory" , v. Nostrand (1950) |
Comments
An outer Carathéodory measure is also frequently called a metric outer measure, cf. [a1].
References
| [a1] | E. Hewitt, K.R. Stromberg, "Real and abstract analysis" , Springer (1965) |
How to Cite This Entry:
Carathéodory measure. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Carath%C3%A9odory_measure&oldid=22247
Carathéodory measure. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Carath%C3%A9odory_measure&oldid=22247
This article was adapted from an original article by V.V. Sazonov (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098. See original article