Difference between revisions of "Constructible subset"
Ulf Rehmann (talk | contribs) m (MR/ZBL numbers added) |
Ulf Rehmann (talk | contribs) m (MR/ZBL numbers added) |
||
| Line 6: | Line 6: | ||
====References==== | ====References==== | ||
| − | <table><TR><TD valign="top">[1]</TD> <TD valign="top"> A. Grothendieck, J. Dieudonné, "Eléments de géometrie algébrique" , '''I. Le langage des schémes''' , Springer (1971) | + | <table><TR><TD valign="top">[1]</TD> <TD valign="top"> A. Grothendieck, J. Dieudonné, "Eléments de géometrie algébrique" , '''I. Le langage des schémes''' , Springer (1971) {{MR|0217085}} {ZBL|0203.23301}} </TD></TR><TR><TD valign="top">[2]</TD> <TD valign="top"> A. Borel, "Linear algebraic groups" , Benjamin (1969) {{MR|0251042}} {{ZBL|0206.49801}} {{ZBL|0186.33201}} </TD></TR></table> |
Revision as of 10:19, 24 March 2012
of an algebraic variety
A finite union of locally closed (in the Zariski topology) subsets. A locally closed subset is, by definition, an intersection of an open and a closed subset. The constructible subsets form a Boolean algebra and can be defined as elements of the Boolean algebra generated by the algebraic subvarieties. The role of constructible subsets in algebraic geometry is revealed by Chevalley's theorem: If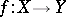 
is a morphism of algebraic varieties, then 
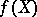(and, moreover, the image of any constructible subset in 
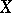) is a constructible subset in 
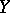. This is related to the fact that "algebraic" conditions determine the constructible subsets of an algebraic variety.
A mapping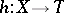 
is called constructible if 
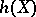is finite and if for any point 
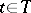the pre-image 
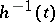is a constructible subset in 
.
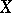References
| [1] | A. Grothendieck, J. Dieudonné, "Eléments de géometrie algébrique" , I. Le langage des schémes , Springer (1971) MR0217085 {ZBL|0203.23301}} |
| [2] | A. Borel, "Linear algebraic groups" , Benjamin (1969) MR0251042 Zbl 0206.49801 Zbl 0186.33201 |
Constructible subset. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Constructible_subset&oldid=21832