Difference between revisions of "Hartogs-Laurent series"
From Encyclopedia of Mathematics
(Importing text file) |
Ulf Rehmann (talk | contribs) m (moved Hartogs–Laurent series to Hartogs-Laurent series: ascii title) |
(No difference)
| |
Revision as of 18:52, 24 March 2012
A series
 | (*) |
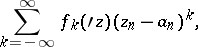where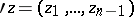 
and where the 
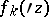are functions holomorphic in some domain 
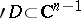which is independent of 
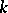. If 
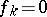for all 
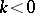, the series (*) is known as a Hartogs series. Any holomorphic function in a Hartogs domain 
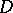of the type
 |
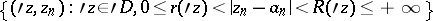can be expanded into a Hartogs–Laurent series which converges absolutely and uniformly inside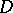 
. In complete Hartogs domains this will be the expansion into a Hartogs series. The domains of convergence of Hartogs–Laurent series are domains of the same kind with special 
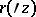and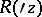 
, known as Hartogs radii. If 
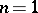, when all 
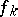are constant, a Hartogs–Laurent series is called a Laurent series.
References
| [1] | V.S. Vladimirov, "Methods of the theory of functions of several complex variables" , M.I.T. (1966) (Translated from Russian) |
Comments
References
| [a1] | H. Behnke, P. Thullen, "Theorie der Funktionen meherer komplexer Veränderlichen" , Springer (1970) (Elraged & Revised Edition. Original: 1934) |
| [a2] | S. Bochner, W.T. Martin, "Several complex variables" , Princeton Univ. Press (1948) |
How to Cite This Entry:
Hartogs-Laurent series. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Hartogs-Laurent_series&oldid=19047
Hartogs-Laurent series. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Hartogs-Laurent_series&oldid=19047
This article was adapted from an original article by E.M. Chirka (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098. See original article