Difference between revisions of "Hilbert-Schmidt series"
From Encyclopedia of Mathematics
(Importing text file) |
Ulf Rehmann (talk | contribs) m (moved Hilbert–Schmidt series to Hilbert-Schmidt series: ascii title) |
(No difference)
| |
Revision as of 18:52, 24 March 2012
A series of functions
 | (*) |
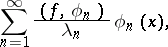where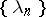 
is the sequence of all eigen values of a symmetric kernel (cf. Kernel of an integral operator) 
, 
, 
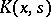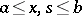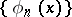is the corresponding sequence of orthonormal eigen functions, while 
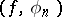is the scalar product of an arbitrary square-summable function 
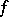and the function 
.
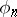The Hilbert–Schmidt theorem: If the kernel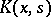 
is a square-summable function in two variables, then the series (*) converges in the mean to the function
 |
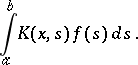If there exists a constant C such that for all 
from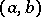 
the inequality
 |
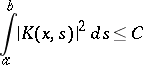is fulfilled, then the Hilbert–Schmidt series converges absolutely and uniformly.
Comments
References
| [a1] | I.C. Gohberg, S. Goldberg, "Basic operator theory" , Birkhäuser (1981) |
How to Cite This Entry:
Hilbert-Schmidt series. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Hilbert-Schmidt_series&oldid=19044
Hilbert-Schmidt series. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Hilbert-Schmidt_series&oldid=19044
This article was adapted from an original article by B.V. Khvedelidze (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098. See original article