Difference between revisions of "Gel'fand representation"
(Importing text file) |
Ulf Rehmann (talk | contribs) m (MR/ZBL numbers added) |
||
| Line 2: | Line 2: | ||
====References==== | ====References==== | ||
| − | <table><TR><TD valign="top">[1]</TD> <TD valign="top"> | + | <table><TR><TD valign="top">[1]</TD> <TD valign="top"> I.M. Gel'fand, "Normierte Ringe" ''Mat. Sb.'' , '''9 (51)''' : 1 (1941) pp. 3–24 {{MR|}} {{ZBL|0134.32102}} {{ZBL|0031.03403}} </TD></TR></table> |
| Line 14: | Line 14: | ||
====References==== | ====References==== | ||
| − | <table><TR><TD valign="top">[a1]</TD> <TD valign="top"> | + | <table><TR><TD valign="top">[a1]</TD> <TD valign="top"> K. Yosida, "Functional analysis" , Springer (1980) pp. Chapt. 8, Sect. 4; 5 {{MR|0617913}} {{ZBL|0435.46002}} </TD></TR><TR><TD valign="top">[a2]</TD> <TD valign="top"> W. Rudin, "Functional analysis" , McGraw-Hill (1979) {{MR|1157815}} {{MR|0458106}} {{MR|0365062}} {{ZBL|0867.46001}} {{ZBL|0253.46001}} </TD></TR></table> |
Revision as of 21:52, 30 March 2012
A mapping establishing a correspondence between an element  of a commutative Banach algebra
of a commutative Banach algebra  and a function
and a function  on the space
on the space  of maximal ideals of
of maximal ideals of  . There exists a one-to-one correspondence between the points of
. There exists a one-to-one correspondence between the points of  and the homomorphisms of
and the homomorphisms of  into the field of complex numbers. If the corresponding identification is made, the Gel'fand representation is realized by the formula
into the field of complex numbers. If the corresponding identification is made, the Gel'fand representation is realized by the formula  . In the special case of the group algebra of a locally compact Abelian group (with convolution taken as multiplication in the algebra, cf. also Group algebra of a locally compact group) the Gel'fand representation coincides with the Fourier transform (for more details see Banach algebra). The Gel'fand transform was introduced by I.M. Gel'fand [1].
. In the special case of the group algebra of a locally compact Abelian group (with convolution taken as multiplication in the algebra, cf. also Group algebra of a locally compact group) the Gel'fand representation coincides with the Fourier transform (for more details see Banach algebra). The Gel'fand transform was introduced by I.M. Gel'fand [1].
References
| [1] | I.M. Gel'fand, "Normierte Ringe" Mat. Sb. , 9 (51) : 1 (1941) pp. 3–24 Zbl 0134.32102 Zbl 0031.03403 |
Comments
The Gel'fand representation is also called the Gel'fand transform, cf. [a2] and Commutative Banach algebra.
Using the Gel'fand representations of specially chosen algebras one can prove various approximation theorems (cf., e.g., [a2], Sect. 11.13). A well-known such theorem is Wiener's theorem (cf. also [a1], Chapt. XI, Sect. 2): If  is a non-vanishing absolutely-convergent (Fourier) series on the interval
is a non-vanishing absolutely-convergent (Fourier) series on the interval  , then
, then 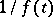 can be represented as an absolutely-convergent Fourier series on this interval.
can be represented as an absolutely-convergent Fourier series on this interval.
In algebraic geometry a very similar representation/transform is used. Let 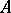 be a commutative ring with unity. To an element
be a commutative ring with unity. To an element 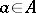 one associates the morphism of affine schemes
one associates the morphism of affine schemes 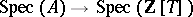 (function) given by the ring homomorphism
(function) given by the ring homomorphism 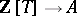 ,
, 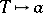 (cf. Affine scheme). In the case of affine varieties over an algebraically closed field
(cf. Affine scheme). In the case of affine varieties over an algebraically closed field 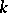 , the function
, the function 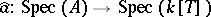 , where now
, where now 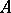 is a
is a  -algebra, takes the value
-algebra, takes the value 
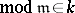 at the closed point of
at the closed point of 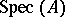 represented by the maximal ideal
represented by the maximal ideal 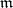 , showing the relationship of this construction with the Gel'fand transform.
, showing the relationship of this construction with the Gel'fand transform.
References
| [a1] | K. Yosida, "Functional analysis" , Springer (1980) pp. Chapt. 8, Sect. 4; 5 MR0617913 Zbl 0435.46002 |
| [a2] | W. Rudin, "Functional analysis" , McGraw-Hill (1979) MR1157815 MR0458106 MR0365062 Zbl 0867.46001 Zbl 0253.46001 |
Gel'fand representation. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Gel%27fand_representation&oldid=18877