Difference between revisions of "Stochastic differential equation"
(Importing text file) |
Ulf Rehmann (talk | contribs) m (MR/ZBL numbers added) |
||
| Line 31: | Line 31: | ||
<table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s090/s090080/s09008046.png" /></td> </tr></table> | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s090/s090080/s09008046.png" /></td> </tr></table> | ||
| − | and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s090/s090080/s09008047.png" />. The term | + | and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s090/s090080/s09008047.png" />. The term "weak solution" sometimes applies only to the process <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s090/s090080/s09008048.png" /> that appears in the set <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s090/s090080/s09008049.png" />. A weak solution of equation (3) exists under weaker hypotheses. It is sufficient, for example, that <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s090/s090080/s09008050.png" />, and that <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s090/s090080/s09008051.png" /> be continuous in <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s090/s090080/s09008052.png" />, that <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s090/s090080/s09008053.png" /> be measurable in <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s090/s090080/s09008054.png" />, and that <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s090/s090080/s09008055.png" />. |
The development of the theory of stochastic integration (see [[Stochastic integral|Stochastic integral]]) using semi-martingales (cf. [[Semi-martingale|Semi-martingale]]) and random measures has led to the study of more general stochastic differential equations, where semi-martingales and random measures are used as generators (along with a Wiener process). The following result is typical. Let <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s090/s090080/s09008056.png" /> be a probability space, let <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s090/s090080/s09008057.png" /> be an increasing family of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s090/s090080/s09008058.png" />-algebras, let <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s090/s090080/s09008059.png" /> be an <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s090/s090080/s09008060.png" />-dimensional semi-martingale, and let <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s090/s090080/s09008061.png" /> be a matrix consisting of non-anticipative functionals <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s090/s090080/s09008062.png" /> such that | The development of the theory of stochastic integration (see [[Stochastic integral|Stochastic integral]]) using semi-martingales (cf. [[Semi-martingale|Semi-martingale]]) and random measures has led to the study of more general stochastic differential equations, where semi-martingales and random measures are used as generators (along with a Wiener process). The following result is typical. Let <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s090/s090080/s09008056.png" /> be a probability space, let <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s090/s090080/s09008057.png" /> be an increasing family of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s090/s090080/s09008058.png" />-algebras, let <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s090/s090080/s09008059.png" /> be an <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s090/s090080/s09008060.png" />-dimensional semi-martingale, and let <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s090/s090080/s09008061.png" /> be a matrix consisting of non-anticipative functionals <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s090/s090080/s09008062.png" /> such that | ||
| Line 50: | Line 50: | ||
====References==== | ====References==== | ||
| − | <table><TR><TD valign="top">[1]</TD> <TD valign="top"> | + | <table><TR><TD valign="top">[1]</TD> <TD valign="top"> I.I. Gikhman, A.V. Skorokhod, "Stochastic differential equations and their applications" , Springer (1972) (Translated from Russian) {{MR|0678374}} {{ZBL|0557.60041}} </TD></TR><TR><TD valign="top">[2]</TD> <TD valign="top"> R.S. Liptser, A.N. Shiryaev, "Statistics of random processes" , '''1–2''' , Springer (1977–1978) (Translated from Russian) {{MR|1800858}} {{MR|1800857}} {{MR|0608221}} {{MR|0488267}} {{MR|0474486}} {{ZBL|1008.62073}} {{ZBL|1008.62072}} {{ZBL|0556.60003}} {{ZBL|0369.60001}} {{ZBL|0364.60004}} </TD></TR></table> |
| Line 58: | Line 58: | ||
====References==== | ====References==== | ||
| − | <table><TR><TD valign="top">[a1]</TD> <TD valign="top"> | + | <table><TR><TD valign="top">[a1]</TD> <TD valign="top"> L. Arnold, "Stochastic differential equations" , Wiley (1974) (Translated from Russian) {{MR|0443083}} {{ZBL|0278.60039}} </TD></TR><TR><TD valign="top">[a2]</TD> <TD valign="top"> H. Bunke, "Gewöhnliche Differentialgleichungen mit zufällige Parametern" , Akademie Verlag (1972) {{MR|423523}} {{ZBL|}} </TD></TR><TR><TD valign="top">[a3]</TD> <TD valign="top"> A. Freedman, "Stochastic differential equations and applications" , '''1''' , Acad. Press (1975)</TD></TR><TR><TD valign="top">[a4]</TD> <TD valign="top"> R.Z. [R.Z. Khasmins'kii] Hasminski, "Stochastic stability of differential equations" , Sijthoff & Noordhoff (1980) (Translated from Russian)</TD></TR><TR><TD valign="top">[a5]</TD> <TD valign="top"> N. Ikeda, S. Watanabe, "Stochastic differential equations and diffusion processes" , North-Holland & Kodansha (1981) {{MR|0637061}} {{ZBL|0495.60005}} </TD></TR><TR><TD valign="top">[a6]</TD> <TD valign="top"> T.T. Soong, "Random differential equations in science and engineering" , Acad. Press (1973) {{MR|0451405}} {{ZBL|0348.60081}} </TD></TR><TR><TD valign="top">[a7]</TD> <TD valign="top"> S.K. Srinivasan, R. Vasudevan, "Introduction to random differential equations and their applications" , Amer. Elsevier (1971) {{MR|0329025}} {{ZBL|0242.60002}} </TD></TR><TR><TD valign="top">[a8]</TD> <TD valign="top"> R.L. Stratonovich, "Topics in the theory of random noise" , '''1–2''' , Gordon & Breach (1963–1967) {{MR|0158437}} {{ZBL|0183.22007}} </TD></TR><TR><TD valign="top">[a9]</TD> <TD valign="top"> D.W. Stroock, S.R.S. Varadhan, "Multidimensional diffusion processes" , Springer (1979) {{MR|0532498}} {{ZBL|0426.60069}} </TD></TR><TR><TD valign="top">[a10]</TD> <TD valign="top"> Th. Gard, "Introduction to stochastic differential equations" , M. Dekker (1988) {{MR|0917064}} {{ZBL|0628.60064}} </TD></TR><TR><TD valign="top">[a11]</TD> <TD valign="top"> B. Øksendahl, "Stochastic differential equations" , Springer (1987)</TD></TR><TR><TD valign="top">[a12]</TD> <TD valign="top"> P. Protter, "Stochastic integration and differential equations" , Springer (1990) {{MR|1037262}} {{ZBL|0694.60047}} </TD></TR><TR><TD valign="top">[a13]</TD> <TD valign="top"> S. Albeverio, M. Röckner, "Stochastic differential equations in infinite dimensions: solutions via Dirichlet forms" ''Probab. Th. Rel. Fields'' , '''89''' (1991) pp. 347–386 {{MR|1113223}} {{ZBL|0725.60055}} </TD></TR><TR><TD valign="top">[a14]</TD> <TD valign="top"> K.D. Elworthy, "Stochastic differential equations on manifolds" , Cambridge Univ. Press (1982) {{MR|0675100}} {{ZBL|0514.58001}} </TD></TR><TR><TD valign="top">[a15]</TD> <TD valign="top"> M. Emery, "Stochastic calculus in manifolds" , Springer (1989) ((Appendix by P.A. Meyer.)) {{MR|1030543}} {{ZBL|0697.60060}} </TD></TR><TR><TD valign="top">[a16]</TD> <TD valign="top"> K. Sobczyk, "Stochastic differential equations. With applications to physics and engineering" , Kluwer (1991) {{MR|1135326}} {{ZBL|0762.60050}} </TD></TR></table> |
Revision as of 10:32, 27 March 2012
for a process  with respect to a Wiener process
with respect to a Wiener process 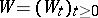
An equation of the form
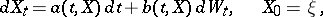 | (1) |
where 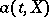 and
and  are non-anticipative functionals, and the random variable
are non-anticipative functionals, and the random variable 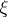 plays the part of the initial value. There are two separate concepts for a solution of a stochastic differential equation — strong and weak.
plays the part of the initial value. There are two separate concepts for a solution of a stochastic differential equation — strong and weak.
Let  be a probability space with an increasing family of
be a probability space with an increasing family of 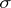 -algebras
-algebras 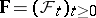 , and let
, and let  be a Wiener process. One says that a continuous stochastic process
be a Wiener process. One says that a continuous stochastic process 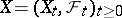 is a strong solution of the stochastic differential equation (1) with drift coefficient
is a strong solution of the stochastic differential equation (1) with drift coefficient 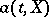 , diffusion coefficient
, diffusion coefficient  and initial value
and initial value 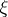 , if for every
, if for every 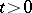 with probability one:
with probability one:
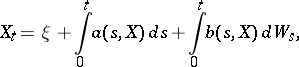 | (2) |
where it is supposed that the integrals in (2) are defined.
The first general result on the existence and uniqueness of a strong solution of a stochastic differential equation of the form
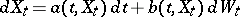 | (3) |
was obtained by K. Itô. He demonstrated that if for every 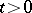 the functions
the functions 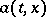 and
and  satisfy a Lipschitz condition with respect to
satisfy a Lipschitz condition with respect to  and increase not faster than linearly, then a continuous solution
and increase not faster than linearly, then a continuous solution 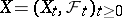 of the equation (3) exists, and this solution is unique in the sense that if
of the equation (3) exists, and this solution is unique in the sense that if  is another continuous solution, then
is another continuous solution, then
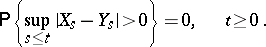 |
If  , the measurability and boundedness of the drift coefficient (vector)
, the measurability and boundedness of the drift coefficient (vector)  guarantees the existence and uniqueness of a strong solution of (3). The equation
guarantees the existence and uniqueness of a strong solution of (3). The equation  , generally speaking, does not have a strong solution for any bounded non-anticipative functional
, generally speaking, does not have a strong solution for any bounded non-anticipative functional  .
.
When studying the concept of a weak solution of the stochastic differential equation (1), the probability space 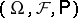 with the family of
with the family of 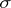 -algebras
-algebras  , the Wiener process
, the Wiener process  and the random variable
and the random variable 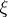 are not fixed in advance, but the non-anticipative functionals
are not fixed in advance, but the non-anticipative functionals 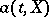 ,
, 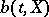 , defined for continuous functions
, defined for continuous functions  , and the distribution function
, and the distribution function 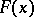 (so to speak, the initial value) are fixed. Then by a weak solution of the equation (1) with given
(so to speak, the initial value) are fixed. Then by a weak solution of the equation (1) with given  ,
,  and
and 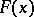 one understands a set of objects
one understands a set of objects
 |
where  is a Wiener process relative to
is a Wiener process relative to 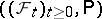 , and
, and 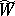 and
and 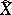 are related by
are related by
 |
and  . The term "weak solution" sometimes applies only to the process
. The term "weak solution" sometimes applies only to the process 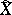 that appears in the set
that appears in the set 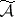 . A weak solution of equation (3) exists under weaker hypotheses. It is sufficient, for example, that
. A weak solution of equation (3) exists under weaker hypotheses. It is sufficient, for example, that 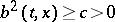 , and that
, and that  be continuous in
be continuous in 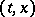 , that
, that 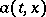 be measurable in
be measurable in 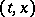 , and that
, and that 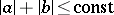 .
.
The development of the theory of stochastic integration (see Stochastic integral) using semi-martingales (cf. Semi-martingale) and random measures has led to the study of more general stochastic differential equations, where semi-martingales and random measures are used as generators (along with a Wiener process). The following result is typical. Let  be a probability space, let
be a probability space, let 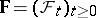 be an increasing family of
be an increasing family of 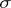 -algebras, let
-algebras, let 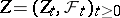 be an
be an 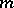 -dimensional semi-martingale, and let
-dimensional semi-martingale, and let  be a matrix consisting of non-anticipative functionals
be a matrix consisting of non-anticipative functionals 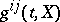 such that
such that
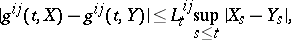 |
where the 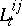 do not increase too rapidly (in
do not increase too rapidly (in 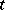 ). Then the stochastic differential equation
). Then the stochastic differential equation  ,
, 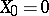 , has a unique strong solution.
, has a unique strong solution.
If the functions 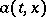 and
and 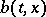 ,
, 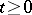 ,
, 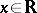 , satisfy a Lipschitz condition (in
, satisfy a Lipschitz condition (in  ) and do not increase faster than linearly, then the solution
) and do not increase faster than linearly, then the solution 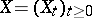 of equation (3) (unique up to stochastic equivalence) will be a Markov process. If, moreover,
of equation (3) (unique up to stochastic equivalence) will be a Markov process. If, moreover, 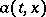 and
and 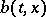 are continuous in all variables, then this will be a diffusion process. Using stochastic differential equations, starting only from a Wiener process, it is thus possible to construct Markov and diffusion processes.
are continuous in all variables, then this will be a diffusion process. Using stochastic differential equations, starting only from a Wiener process, it is thus possible to construct Markov and diffusion processes.
Given certain extra conditions of smoothness on the functions 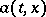 and
and 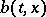 , the solution
, the solution  of equation (3) with initial condition
of equation (3) with initial condition 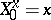 is such that the function
is such that the function  , given a sufficiently smooth function
, given a sufficiently smooth function 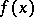 , satisfies the backward Kolmogorov equation
, satisfies the backward Kolmogorov equation
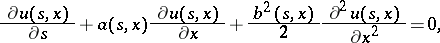 |
in the domain 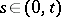 ,
,  , with the boundary condition
, with the boundary condition
 |
References
| [1] | I.I. Gikhman, A.V. Skorokhod, "Stochastic differential equations and their applications" , Springer (1972) (Translated from Russian) MR0678374 Zbl 0557.60041 |
| [2] | R.S. Liptser, A.N. Shiryaev, "Statistics of random processes" , 1–2 , Springer (1977–1978) (Translated from Russian) MR1800858 MR1800857 MR0608221 MR0488267 MR0474486 Zbl 1008.62073 Zbl 1008.62072 Zbl 0556.60003 Zbl 0369.60001 Zbl 0364.60004 |
Comments
References
| [a1] | L. Arnold, "Stochastic differential equations" , Wiley (1974) (Translated from Russian) MR0443083 Zbl 0278.60039 |
| [a2] | H. Bunke, "Gewöhnliche Differentialgleichungen mit zufällige Parametern" , Akademie Verlag (1972) MR423523 |
| [a3] | A. Freedman, "Stochastic differential equations and applications" , 1 , Acad. Press (1975) |
| [a4] | R.Z. [R.Z. Khasmins'kii] Hasminski, "Stochastic stability of differential equations" , Sijthoff & Noordhoff (1980) (Translated from Russian) |
| [a5] | N. Ikeda, S. Watanabe, "Stochastic differential equations and diffusion processes" , North-Holland & Kodansha (1981) MR0637061 Zbl 0495.60005 |
| [a6] | T.T. Soong, "Random differential equations in science and engineering" , Acad. Press (1973) MR0451405 Zbl 0348.60081 |
| [a7] | S.K. Srinivasan, R. Vasudevan, "Introduction to random differential equations and their applications" , Amer. Elsevier (1971) MR0329025 Zbl 0242.60002 |
| [a8] | R.L. Stratonovich, "Topics in the theory of random noise" , 1–2 , Gordon & Breach (1963–1967) MR0158437 Zbl 0183.22007 |
| [a9] | D.W. Stroock, S.R.S. Varadhan, "Multidimensional diffusion processes" , Springer (1979) MR0532498 Zbl 0426.60069 |
| [a10] | Th. Gard, "Introduction to stochastic differential equations" , M. Dekker (1988) MR0917064 Zbl 0628.60064 |
| [a11] | B. Øksendahl, "Stochastic differential equations" , Springer (1987) |
| [a12] | P. Protter, "Stochastic integration and differential equations" , Springer (1990) MR1037262 Zbl 0694.60047 |
| [a13] | S. Albeverio, M. Röckner, "Stochastic differential equations in infinite dimensions: solutions via Dirichlet forms" Probab. Th. Rel. Fields , 89 (1991) pp. 347–386 MR1113223 Zbl 0725.60055 |
| [a14] | K.D. Elworthy, "Stochastic differential equations on manifolds" , Cambridge Univ. Press (1982) MR0675100 Zbl 0514.58001 |
| [a15] | M. Emery, "Stochastic calculus in manifolds" , Springer (1989) ((Appendix by P.A. Meyer.)) MR1030543 Zbl 0697.60060 |
| [a16] | K. Sobczyk, "Stochastic differential equations. With applications to physics and engineering" , Kluwer (1991) MR1135326 Zbl 0762.60050 |
Stochastic differential equation. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Stochastic_differential_equation&oldid=18807