Difference between revisions of "Spinor group"
(Importing text file) |
Ulf Rehmann (talk | contribs) m (MR/ZBL numbers added) |
||
| Line 44: | Line 44: | ||
====References==== | ====References==== | ||
| − | <table><TR><TD valign="top">[1]</TD> <TD valign="top"> | + | <table><TR><TD valign="top">[1]</TD> <TD valign="top"> H. Weyl, "The classical groups, their invariants and representations" , Princeton Univ. Press (1946) {{MR|0000255}} {{ZBL|1024.20502}} </TD></TR><TR><TD valign="top">[2]</TD> <TD valign="top"> J.A. Dieudonné, "La géométrie des groups classiques" , Springer (1955) {{MR|}} {{ZBL|0221.20056}} </TD></TR><TR><TD valign="top">[3]</TD> <TD valign="top"> E. Cartan, "Leçons sur la théorie des spineurs" , '''2''' , Hermann (1938) {{MR|}} {{ZBL|0022.17101}} {{ZBL|0019.36301}} {{ZBL|64.1382.04}} </TD></TR><TR><TD valign="top">[4]</TD> <TD valign="top"> M.M. Postnikov, "Lie groups and Lie algebras" , Moscow (1982) (In Russian) {{MR|0905471}} {{ZBL|0597.22001}} </TD></TR><TR><TD valign="top">[5]</TD> <TD valign="top"> C. Chevalley, "Theory of Lie groups" , '''1''' , Princeton Univ. Press (1946) {{MR|0082628}} {{MR|0015396}} {{ZBL|0063.00842}} </TD></TR></table> |
| Line 54: | Line 54: | ||
====References==== | ====References==== | ||
| − | <table><TR><TD valign="top">[a1]</TD> <TD valign="top"> | + | <table><TR><TD valign="top">[a1]</TD> <TD valign="top"> N. Bourbaki, "Algèbre. Formes sesquilineares et formes quadratiques" , ''Eléments de mathématiques'' , Hermann (1959) pp. Chapt. 9 {{MR|0174550}} {{MR|0107661}} {{ZBL|}} </TD></TR><TR><TD valign="top">[a2]</TD> <TD valign="top"> C. Chevalley, "The algebraic theory of spinors" , Columbia Univ. Press (1954) {{MR|0060497}} {{ZBL|0057.25901}} </TD></TR><TR><TD valign="top">[a3]</TD> <TD valign="top"> Th. Bröcker, T. Tom Dieck, "Representations of compact Lie groups" , Springer (1985) {{MR|0781344}} {{ZBL|0581.22009}} </TD></TR></table> |
Revision as of 14:52, 24 March 2012
of a non-generate quadratic form 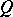 on an
on an  -dimensional vector space
-dimensional vector space 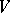 (
(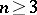 ) over a field
) over a field 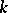
A connected linear algebraic group which is the simply-connected covering of the irreducible component 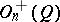 of the identity of the orthogonal group
of the identity of the orthogonal group 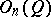 of the form
of the form 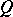 . If
. If 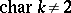 , then
, then 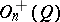 coincides with the special orthogonal group
coincides with the special orthogonal group 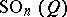 . The spinor group is constructed in the following way. Let
. The spinor group is constructed in the following way. Let 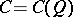 be the Clifford algebra of the pair
be the Clifford algebra of the pair 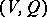 , let
, let 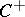 (
(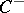 ) be the subspace of
) be the subspace of 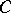 generated by products of an even (odd) number of elements of
generated by products of an even (odd) number of elements of 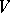 , and let
, and let 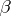 be the canonical anti-automorphism of
be the canonical anti-automorphism of 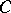 defined by the formula
defined by the formula
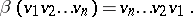 |
The inclusion 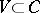 enables one to define the Clifford group
enables one to define the Clifford group
 |
and the even (or special) Clifford group
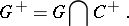 |
The spinor group 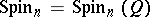 is defined by
is defined by
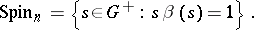 |
The spinor group 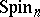 is a quasi-simple (when
is a quasi-simple (when 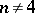 ), connected, simply-connected, linear algebraic group, of type
), connected, simply-connected, linear algebraic group, of type 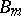 when
when 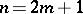 and of type
and of type 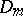 when
when  ; if
; if 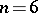 it is
it is 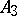 and if
and if 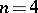 it is
it is 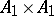 . The following isomorphisms hold:
. The following isomorphisms hold:
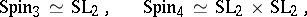 |
 |
There is a linear representation 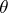 of
of 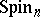 in
in 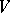 defined by
defined by
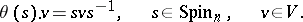 |
If 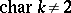 ,
,
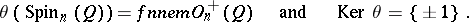 |
The group 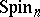 has a faithful linear representation in
has a faithful linear representation in 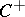 (see Spinor representation).
(see Spinor representation).
If 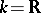 is the field of real numbers and
is the field of real numbers and 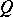 is positive (or negative) definite, then the group
is positive (or negative) definite, then the group 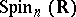 of real points of the algebraic group
of real points of the algebraic group 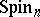 is sometimes also called a spinor group. This is a connected simply-connected compact Lie group which is a two-sheeted covering of the special orthogonal group
is sometimes also called a spinor group. This is a connected simply-connected compact Lie group which is a two-sheeted covering of the special orthogonal group 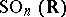 . The following isomorphisms hold:
. The following isomorphisms hold:
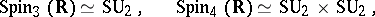 |
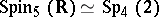 |
(see Symplectic group),
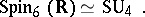 |
References
| [1] | H. Weyl, "The classical groups, their invariants and representations" , Princeton Univ. Press (1946) MR0000255 Zbl 1024.20502 |
| [2] | J.A. Dieudonné, "La géométrie des groups classiques" , Springer (1955) Zbl 0221.20056 |
| [3] | E. Cartan, "Leçons sur la théorie des spineurs" , 2 , Hermann (1938) Zbl 0022.17101 Zbl 0019.36301 Zbl 64.1382.04 |
| [4] | M.M. Postnikov, "Lie groups and Lie algebras" , Moscow (1982) (In Russian) MR0905471 Zbl 0597.22001 |
| [5] | C. Chevalley, "Theory of Lie groups" , 1 , Princeton Univ. Press (1946) MR0082628 MR0015396 Zbl 0063.00842 |
Comments
See also Quadratic form.
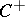 is the so-called even Clifford algebra of
is the so-called even Clifford algebra of 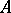 .
.
References
| [a1] | N. Bourbaki, "Algèbre. Formes sesquilineares et formes quadratiques" , Eléments de mathématiques , Hermann (1959) pp. Chapt. 9 MR0174550 MR0107661 |
| [a2] | C. Chevalley, "The algebraic theory of spinors" , Columbia Univ. Press (1954) MR0060497 Zbl 0057.25901 |
| [a3] | Th. Bröcker, T. Tom Dieck, "Representations of compact Lie groups" , Springer (1985) MR0781344 Zbl 0581.22009 |
Spinor group. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Spinor_group&oldid=18620