Difference between revisions of "Frénet formulas"
From Encyclopedia of Mathematics
(Importing text file) |
Ulf Rehmann (talk | contribs) m (moved Frénet formulas to Frenet formulas: ascii title) |
(No difference)
| |
Revision as of 18:52, 24 March 2012
Formulas that express the derivatives of the unit vectors of the tangent  , the normal
, the normal  and the binormal
and the binormal 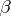 to a regular curve with respect to the natural parameter
to a regular curve with respect to the natural parameter  in terms of these same vectors and the values of the curvature
in terms of these same vectors and the values of the curvature 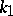 and torsion
and torsion 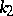 of the curve:
of the curve:
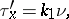 |
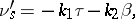 |
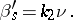 |
They were obtained by F. Frénet (1847).
Comments
References
| [a1] | C.C. Hsiung, "A first course in differential geometry" , Wiley (1981) pp. Chapt. 3, Sect. 4 |
How to Cite This Entry:
Frénet formulas. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Fr%C3%A9net_formulas&oldid=17588
Frénet formulas. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Fr%C3%A9net_formulas&oldid=17588
This article was adapted from an original article by D.D. Sokolov (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098. See original article