Difference between revisions of "Point in general position"
(Importing text file) |
Ulf Rehmann (talk | contribs) m (MR/ZBL numbers added) |
||
| Line 6: | Line 6: | ||
More precisely, a point is said to be in general position if it is outside a certain (given, or to be described) closed set; a point in an irreducible set <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p073/p073170/p0731702.png" /> is called generic if it is outside every closed set different from <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p073/p073170/p0731703.png" /> itself. | More precisely, a point is said to be in general position if it is outside a certain (given, or to be described) closed set; a point in an irreducible set <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p073/p073170/p0731702.png" /> is called generic if it is outside every closed set different from <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p073/p073170/p0731703.png" /> itself. | ||
| − | In differential topology, the phrase | + | In differential topology, the phrase "a point in general position" often is used in the sense of a generic point, which is roughly "a point with no particular relationship of current importance to other structure elements being considered" . The precise meaning depends on the context. An element generically has a certain property if the property holds outside (a countable intersection of) open dense set(s). For instance, a polynomial has generically no double roots. Two submanifolds <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p073/p073170/p0731704.png" /> are in general position if they "intersect as little as possible" . If <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p073/p073170/p0731705.png" />, this means <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p073/p073170/p0731706.png" />; if <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p073/p073170/p0731707.png" />, then for every <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p073/p073170/p0731708.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p073/p073170/p0731709.png" />. Any non-general position situation can be changed to a general position situation by an arbitrarily small change, while if things are in general position, then sufficiently small changes do not change that. A precise version of general position is [[Transversality|transversality]], cf. also [[Transversality condition|Transversality condition]]. |
====References==== | ====References==== | ||
| − | <table><TR><TD valign="top">[a1]</TD> <TD valign="top"> | + | <table><TR><TD valign="top">[a1]</TD> <TD valign="top"> R. Hartshorne, "Algebraic geometry" , Springer (1977) pp. 91 {{MR|0463157}} {{ZBL|0367.14001}} </TD></TR><TR><TD valign="top">[a2]</TD> <TD valign="top"> M.W. Hirsch, "Differential topology" , Springer (1976) pp. 4, 78 {{MR|0448362}} {{ZBL|0356.57001}} </TD></TR><TR><TD valign="top">[a3]</TD> <TD valign="top"> D.R.J. Chillingworth, "Differential topology with a view to applications" , Pitman (1976) pp. 221ff {{MR|0646088}} {{ZBL|0336.58001}} </TD></TR></table> |
Revision as of 21:55, 30 March 2012
A point on an algebraic variety that belongs to an open and dense subset  in the Zariski topology. In algebraic geometry a point in general position is often called simply a generic point.
in the Zariski topology. In algebraic geometry a point in general position is often called simply a generic point.
Comments
More precisely, a point is said to be in general position if it is outside a certain (given, or to be described) closed set; a point in an irreducible set 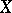 is called generic if it is outside every closed set different from
is called generic if it is outside every closed set different from 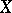 itself.
itself.
In differential topology, the phrase "a point in general position" often is used in the sense of a generic point, which is roughly "a point with no particular relationship of current importance to other structure elements being considered" . The precise meaning depends on the context. An element generically has a certain property if the property holds outside (a countable intersection of) open dense set(s). For instance, a polynomial has generically no double roots. Two submanifolds  are in general position if they "intersect as little as possible" . If
are in general position if they "intersect as little as possible" . If 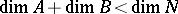 , this means
, this means  ; if
; if 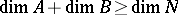 , then for every
, then for every 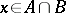 ,
, 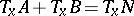 . Any non-general position situation can be changed to a general position situation by an arbitrarily small change, while if things are in general position, then sufficiently small changes do not change that. A precise version of general position is transversality, cf. also Transversality condition.
. Any non-general position situation can be changed to a general position situation by an arbitrarily small change, while if things are in general position, then sufficiently small changes do not change that. A precise version of general position is transversality, cf. also Transversality condition.
References
| [a1] | R. Hartshorne, "Algebraic geometry" , Springer (1977) pp. 91 MR0463157 Zbl 0367.14001 |
| [a2] | M.W. Hirsch, "Differential topology" , Springer (1976) pp. 4, 78 MR0448362 Zbl 0356.57001 |
| [a3] | D.R.J. Chillingworth, "Differential topology with a view to applications" , Pitman (1976) pp. 221ff MR0646088 Zbl 0336.58001 |
Point in general position. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Point_in_general_position&oldid=17545