Difference between revisions of "Finite-to-one mapping"
(Importing text file) |
Ulf Rehmann (talk | contribs) m (MR/ZBL numbers added) |
||
| Line 6: | Line 6: | ||
====References==== | ====References==== | ||
| − | <table><TR><TD valign="top">[1]</TD> <TD valign="top"> | + | <table><TR><TD valign="top">[1]</TD> <TD valign="top"> A.V. Arkhangel'skii, V.I. Ponomarev, "Fundamentals of general topology: problems and exercises" , Reidel (1984) (Translated from Russian) {{MR|785749}} {{ZBL|0568.54001}} </TD></TR><TR><TD valign="top">[2]</TD> <TD valign="top"> M. Golubitsky, "Stable mappings and their singularities" , Springer (1973) {{MR|0341518}} {{ZBL|0294.58004}} </TD></TR></table> |
| Line 16: | Line 16: | ||
====References==== | ====References==== | ||
| − | <table><TR><TD valign="top">[a1]</TD> <TD valign="top"> | + | <table><TR><TD valign="top">[a1]</TD> <TD valign="top"> V.I. Arnol'd, S.M. [S.M. Khusein-Zade] Gusein-Zade, A.N. Varchenko, "Singularities of differentiable maps" , '''1''' , Birkhäuser (1985) (Translated from Russian) {{MR|777682}} {{ZBL|0554.58001}} </TD></TR></table> |
Revision as of 16:57, 15 April 2012
A mapping 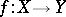 such that the number
such that the number 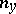 of points in the pre-image
of points in the pre-image 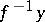 of every point
of every point 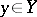 is finite. If
is finite. If 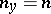 is the same for all
is the same for all 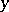 ,
, 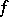 is said to be an
is said to be an  -to-one mapping.
-to-one mapping.
In the differentiable case, the concept of a finite-to-one mapping corresponds to that of a finite mapping. A differentiable mapping 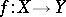 of differentiable manifolds is said to be finite at a point
of differentiable manifolds is said to be finite at a point 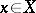 if the dimension of the local ring
if the dimension of the local ring 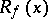 of
of 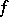 at
at  is finite. All mappings of this sort are finite-to-one mappings on compact subsets of
is finite. All mappings of this sort are finite-to-one mappings on compact subsets of 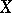 ; moreover, there exists an open neighbourhood
; moreover, there exists an open neighbourhood 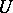 of
of  such that
such that 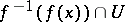 consists of a single point. The number
consists of a single point. The number 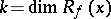 measures the multiplicity of
measures the multiplicity of  as a root of the equation
as a root of the equation 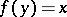 ; there exists a neighbourhood
; there exists a neighbourhood 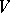 of
of  such that
such that 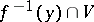 has at most
has at most 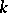 points for every
points for every 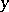 sufficiently close to
sufficiently close to  .
.
If 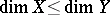 , the finite mappings form a generic set in the space
, the finite mappings form a generic set in the space 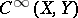 ; moreover, the set of non-finite mappings has infinite codimension in that space (Tougeron's theorem).
; moreover, the set of non-finite mappings has infinite codimension in that space (Tougeron's theorem).
References
| [1] | A.V. Arkhangel'skii, V.I. Ponomarev, "Fundamentals of general topology: problems and exercises" , Reidel (1984) (Translated from Russian) MR785749 Zbl 0568.54001 |
| [2] | M. Golubitsky, "Stable mappings and their singularities" , Springer (1973) MR0341518 Zbl 0294.58004 |
Comments
Let 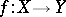 be a mapping of differentiable manifolds. For
be a mapping of differentiable manifolds. For 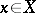 let
let 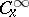 denote the ring of germs of smooth functions
denote the ring of germs of smooth functions 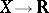 at
at  . This is a local ring with maximal ideal
. This is a local ring with maximal ideal 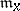 consisting of all germs vanishing at
consisting of all germs vanishing at  . If
. If 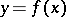 , then by pullback,
, then by pullback, 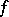 induces a ring homomorphism
induces a ring homomorphism 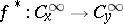 . The local ring of the mapping
. The local ring of the mapping 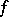 is now defined as the quotient ring
is now defined as the quotient ring 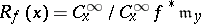 .
.
If 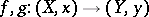 are germs of stable mappings then
are germs of stable mappings then 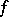 and
and 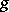 are equivalent if and only if
are equivalent if and only if 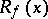 and
and 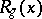 are isomorphic as rings (Mather's theorem). Here equivalence of germs of mappings
are isomorphic as rings (Mather's theorem). Here equivalence of germs of mappings 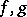 means that there exist germs of diffeomorphisms
means that there exist germs of diffeomorphisms 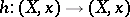 and
and 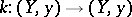 such that
such that 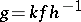 (near
(near  ).
).
References
| [a1] | V.I. Arnol'd, S.M. [S.M. Khusein-Zade] Gusein-Zade, A.N. Varchenko, "Singularities of differentiable maps" , 1 , Birkhäuser (1985) (Translated from Russian) MR777682 Zbl 0554.58001 |
Finite-to-one mapping. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Finite-to-one_mapping&oldid=17330