Difference between revisions of "Implicit function (in algebraic geometry)"
(Importing text file) |
Ulf Rehmann (talk | contribs) m (MR/ZBL numbers added) |
||
| Line 18: | Line 18: | ||
====References==== | ====References==== | ||
| − | <table><TR><TD valign="top">[1]</TD> <TD valign="top"> | + | <table><TR><TD valign="top">[1]</TD> <TD valign="top"> M. Artin, "Algebraic spaces" , Yale Univ. Press (1971) {{MR|0427316}} {{MR|0407012}} {{ZBL|0232.14003}} {{ZBL|0226.14001}} {{ZBL|0216.05501}} </TD></TR><TR><TD valign="top">[2]</TD> <TD valign="top"> M. Artin, "Algebraic approximation of structures over complete local rings" ''Publ. Math. IHES'' , '''36''' (1969) pp. 23–58 {{MR|0268188}} {{ZBL|0181.48802}} </TD></TR><TR><TD valign="top">[3]</TD> <TD valign="top"> M. Artin, "On the solution of algebraic equations" ''Invent. Math.'' , '''5''' (1968) pp. 277–291</TD></TR></table> |
Revision as of 21:53, 30 March 2012
A function given by an algebraic equation. Let  be a polynomial in
be a polynomial in  and
and  (with complex coefficients, say). Then the variety
(with complex coefficients, say). Then the variety  of zeros of this polynomial can be regarded as the graph of a correspondence
of zeros of this polynomial can be regarded as the graph of a correspondence  . This correspondence, allowing for a certain impreciseness, is also called the function given implicitly by the equation
. This correspondence, allowing for a certain impreciseness, is also called the function given implicitly by the equation  . Generally speaking,
. Generally speaking,  is many-valued and not defined everywhere and so is not a function in the usual sense. There are two ways of turning this correspondence into a function. The first, which goes back to B. Riemann, consists in assuming that the domain of definition of the implicit function
is many-valued and not defined everywhere and so is not a function in the usual sense. There are two ways of turning this correspondence into a function. The first, which goes back to B. Riemann, consists in assuming that the domain of definition of the implicit function  is not
is not  but the variety
but the variety  , which is a finite-sheeted covering of
, which is a finite-sheeted covering of  . This device leads to the highly important concept of a Riemann surface. In this approach the notion of an implicit function interlinks with that of an algebraic function.
. This device leads to the highly important concept of a Riemann surface. In this approach the notion of an implicit function interlinks with that of an algebraic function.
The other approach consists in representing  locally as the graph of a single-valued function. Various implicit-function theorems assert that there are open sets
locally as the graph of a single-valued function. Various implicit-function theorems assert that there are open sets  and
and  for which
for which  is the graph of a smooth function (in one sense or another)
is the graph of a smooth function (in one sense or another)  (see Implicit function). However, the open sets
(see Implicit function). However, the open sets 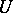 and
and 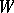 are, as a rule, not open in the Zariski topology and have no meaning in algebraic geometry. Therefore, one modifies this method in the following manner. A formal germ (or branch) at a point
are, as a rule, not open in the Zariski topology and have no meaning in algebraic geometry. Therefore, one modifies this method in the following manner. A formal germ (or branch) at a point  of the implicit function given by the equation
of the implicit function given by the equation  is defined as a formal power series
is defined as a formal power series  such that
such that  . Quite generally, a power series
. Quite generally, a power series  satisfying a polynomial equation
satisfying a polynomial equation  is said to be algebraic. An algebraic power series converges in a certain neighbourhood of
is said to be algebraic. An algebraic power series converges in a certain neighbourhood of  .
.
Let  be a local Noetherian ring with maximal ideal
be a local Noetherian ring with maximal ideal  . An element
. An element  of the completion
of the completion 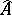 of
of  is said to be algebraic over
is said to be algebraic over  if
if 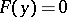 for some polynomial
for some polynomial  . The set of elements of
. The set of elements of  that are algebraic over
that are algebraic over  forms a ring
forms a ring  . The following version of the implicit-function theorem shows that there are sufficiently many algebraic functions. Let
. The following version of the implicit-function theorem shows that there are sufficiently many algebraic functions. Let
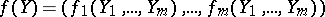 |
be a collection of 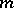 polynomials from
polynomials from  and let
and let  be elements of the residue class field
be elements of the residue class field  (the bar above a letter means reduction
(the bar above a letter means reduction  ) such that:
) such that:
1) 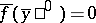 ;
;
2)  .
.
Then there exist elements  algebraic over
algebraic over  such that
such that  and
and 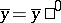 . In other words,
. In other words,  is a Hensel ring.
is a Hensel ring.
Another result of this type is Artin's approximation theorem (see [2]). Let 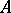 be a local ring that is the localization of an algebra of finite type over a field. Next, let
be a local ring that is the localization of an algebra of finite type over a field. Next, let  be a system of polynomial equations with coefficients in
be a system of polynomial equations with coefficients in  (or in
(or in  ) and let
) and let 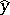 be a vector with coefficients in
be a vector with coefficients in  such that
such that 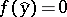 . Then there is a vector
. Then there is a vector 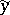 with components in
with components in  , arbitrarily close to
, arbitrarily close to 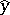 and such that
and such that  . There is also a version [3] of this theorem for systems of analytic equations.
. There is also a version [3] of this theorem for systems of analytic equations.
References
| [1] | M. Artin, "Algebraic spaces" , Yale Univ. Press (1971) MR0427316 MR0407012 Zbl 0232.14003 Zbl 0226.14001 Zbl 0216.05501 |
| [2] | M. Artin, "Algebraic approximation of structures over complete local rings" Publ. Math. IHES , 36 (1969) pp. 23–58 MR0268188 Zbl 0181.48802 |
| [3] | M. Artin, "On the solution of algebraic equations" Invent. Math. , 5 (1968) pp. 277–291 |
Implicit function (in algebraic geometry). Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Implicit_function_(in_algebraic_geometry)&oldid=16421