Difference between revisions of "Completely-continuous operator"
(Importing text file) |
Wf6humboldt (talk | contribs) |
||
| Line 1: | Line 1: | ||
| − | |||
| − | |||
| − | + | ||
| + | ''Completely-Continuous Operator'' | ||
| + | |||
| + | A bounded linear operator <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c023/c023950/c0239501.png" />, acting from a [[Banach space|Banach space]] <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c023/c023950/c0239502.png" /> into another space <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c023/c023950/c0239503.png" />, that transforms weakly-convergent sequences in <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c023/c023950/c0239504.png" /> to norm-convergent sequences in <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c023/c023950/c0239505.png" />. Equivalently, an operator <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c023/c023950/c0239508.png" /> is completely-continuous if it maps every relatively weakly compact subset of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c023/c023950/c0239509.png" /> into a relatively compact subset of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c023/c023950/c02395010.png" />. It is easy to see that every compact operator is completely continuous, however the converse is false. For example, recall that the Banach space ''X'' = ''l''<sub>1</sub> has the Schur Property, that is weak sequential and norm sequential convergence coincide. It follows that the identity operator from ''X'' to ''X'' is completely-continuous, but it is not compact since ''X'' is infinite-dimensional. If ''X'' is reflexive, then every completely-continuous operator is compact, so the two classes of operators do coincide in that case. In the past, the term "completely-continuous operator" was often used to mean compact operator which has sometimes resulted in confusion. | ||
| + | |||
| + | It can be assumed that the space <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c023/c023950/c0239506.png" /> is separable (for <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c023/c023950/c0239507.png" /> this is not a necessary condition; however, the image of a completely-continuous operator is always separable). | ||
| + | |||
| + | |||
| + | The class of compact operators is the most important class of the set of completely-continuous operators (cf. [[Compact operator|Compact operator]]). | ||
| + | |||
====References==== | ====References==== | ||
| Line 11: | Line 18: | ||
====Comments==== | ====Comments==== | ||
| − | + | ||
====References==== | ====References==== | ||
<table><TR><TD valign="top">[a1]</TD> <TD valign="top"> N. Dunford, J.T. Schwartz, "Linear operators. General theory" , '''1''' , Interscience (1958)</TD></TR><TR><TD valign="top">[a2]</TD> <TD valign="top"> A.E. Taylor, D.C. Lay, "Introduction to functional analysis" , Wiley (1980)</TD></TR></table> | <table><TR><TD valign="top">[a1]</TD> <TD valign="top"> N. Dunford, J.T. Schwartz, "Linear operators. General theory" , '''1''' , Interscience (1958)</TD></TR><TR><TD valign="top">[a2]</TD> <TD valign="top"> A.E. Taylor, D.C. Lay, "Introduction to functional analysis" , Wiley (1980)</TD></TR></table> | ||
Revision as of 02:14, 31 March 2013
Completely-Continuous Operator
A bounded linear operator  , acting from a Banach space
, acting from a Banach space  into another space
into another space  , that transforms weakly-convergent sequences in
, that transforms weakly-convergent sequences in  to norm-convergent sequences in
to norm-convergent sequences in  . Equivalently, an operator
. Equivalently, an operator  is completely-continuous if it maps every relatively weakly compact subset of
is completely-continuous if it maps every relatively weakly compact subset of  into a relatively compact subset of
into a relatively compact subset of 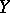 . It is easy to see that every compact operator is completely continuous, however the converse is false. For example, recall that the Banach space X = l1 has the Schur Property, that is weak sequential and norm sequential convergence coincide. It follows that the identity operator from X to X is completely-continuous, but it is not compact since X is infinite-dimensional. If X is reflexive, then every completely-continuous operator is compact, so the two classes of operators do coincide in that case. In the past, the term "completely-continuous operator" was often used to mean compact operator which has sometimes resulted in confusion.
. It is easy to see that every compact operator is completely continuous, however the converse is false. For example, recall that the Banach space X = l1 has the Schur Property, that is weak sequential and norm sequential convergence coincide. It follows that the identity operator from X to X is completely-continuous, but it is not compact since X is infinite-dimensional. If X is reflexive, then every completely-continuous operator is compact, so the two classes of operators do coincide in that case. In the past, the term "completely-continuous operator" was often used to mean compact operator which has sometimes resulted in confusion.
It can be assumed that the space  is separable (for
is separable (for  this is not a necessary condition; however, the image of a completely-continuous operator is always separable).
this is not a necessary condition; however, the image of a completely-continuous operator is always separable).
The class of compact operators is the most important class of the set of completely-continuous operators (cf. Compact operator).
References
| [1] | D. Hilbert, "Grundzüge einer allgemeinen Theorie der linearen Integralgleichungen" , Chelsea, reprint (1953) |
| [2] | F. Riesz, "Sur les opérations fonctionelles linéaires" C.R. Acad. Sci. Paris Sér. I Math. , 149 (1909) pp. 974–977 |
| [3] | S.S. Banach, "Théorie des opérations linéaires" , Hafner (1932) |
Comments
References
| [a1] | N. Dunford, J.T. Schwartz, "Linear operators. General theory" , 1 , Interscience (1958) |
| [a2] | A.E. Taylor, D.C. Lay, "Introduction to functional analysis" , Wiley (1980) |
Completely-continuous operator. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Completely-continuous_operator&oldid=16228