Difference between revisions of "Stationary phase, method of the"
(Importing text file) |
Ulf Rehmann (talk | contribs) m (MR/ZBL numbers added) |
||
| Line 40: | Line 40: | ||
====References==== | ====References==== | ||
| − | <table><TR><TD valign="top">[1]</TD> <TD valign="top"> | + | <table><TR><TD valign="top">[1]</TD> <TD valign="top"> W. Thomson, ''Philos. Mag.'' , '''23''' (1887) pp. 252–255</TD></TR><TR><TD valign="top">[2]</TD> <TD valign="top"> A. Erdélyi, "Asymptotic expansions" , Dover, reprint (1956) {{MR|0081379}} {{MR|0078494}} {{ZBL|0072.11703}} {{ZBL|0070.29002}} </TD></TR><TR><TD valign="top">[3]</TD> <TD valign="top"> E.Ya. Rieksteyn'sh, "Asymptotic expansions of integrals" , '''1–2''' , Riga (1974–1977) (In Russian)</TD></TR><TR><TD valign="top">[4]</TD> <TD valign="top"> F.W.J. Olver, "Asymptotics and special functions" , Acad. Press (1974) {{MR|0435697}} {{ZBL|0308.41023}} {{ZBL|0303.41035}} </TD></TR><TR><TD valign="top">[5]</TD> <TD valign="top"> M.V. Fedoryuk, "The method of steepest descent" , Moscow (1977) (In Russian)</TD></TR><TR><TD valign="top">[6]</TD> <TD valign="top"> M.F. Atiyah, "Resolution of singularities and division of distributions" ''Comm. Pure Appl. Math.'' , '''23''' : 2 (1970) pp. 145–150 {{MR|0256156}} {{ZBL|0188.19405}} </TD></TR><TR><TD valign="top">[7]</TD> <TD valign="top"> V.I. Arnol'd, "Remarks on the stationary phase method and Coxeter numbers" ''Russian Math. Surveys'' , '''28''' : 5 (1973) pp. 19–48 ''Uspekhi Mat. Nauk'' , '''28''' : 5 (1973) pp. 17–44 {{MR|}} {{ZBL|0291.40005}} </TD></TR><TR><TD valign="top">[8]</TD> <TD valign="top"> A.N. Varchenko, "Newton polyhedra and estimation of oscillating integrals" ''Funct. Anal. Appl'' , '''10''' : 3 (1976) pp. 175–196 ''Funktsional. Anal. i Prilozhen.'' , '''10''' : 3 (1976) pp. 13–38 {{MR|}} {{ZBL|0351.32011}} </TD></TR><TR><TD valign="top">[9]</TD> <TD valign="top"> V.P. Maslov, M.V. Fedoryuk, "Semi-classical approximation in quantum mechanics" , Reidel (1981) (Translated from Russian) {{MR|}} {{ZBL|0458.58001}} </TD></TR><TR><TD valign="top">[10]</TD> <TD valign="top"> M.V. Fedoryuk, "Asymptotics. Integrals and series" , Moscow (1987) (In Russian) {{MR|0950167}} {{ZBL|0641.41001}} </TD></TR></table> |
| Line 48: | Line 48: | ||
====References==== | ====References==== | ||
| − | <table><TR><TD valign="top">[a1]</TD> <TD valign="top"> | + | <table><TR><TD valign="top">[a1]</TD> <TD valign="top"> R. Wong, "Asymptotic approximations of integrals" , Acad. Press (1989) {{MR|1016818}} {{ZBL|0679.41001}} </TD></TR><TR><TD valign="top">[a2]</TD> <TD valign="top"> L.V. Hörmander, "The analysis of linear partial differential operators" , '''1''' , Springer (1983) pp. §7.7 {{MR|0717035}} {{MR|0705278}} {{ZBL|0521.35002}} {{ZBL|0521.35001}} </TD></TR></table> |
Revision as of 17:01, 15 April 2012
A method for calculating the asymptotics of integrals of rapidly-oscillating functions:
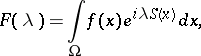 | (*) |
where  ,
,  ,
, 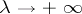 , is a large parameter,
, is a large parameter,  is a bounded domain, the function
is a bounded domain, the function 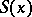 (the phase) is real, the function
(the phase) is real, the function 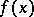 is complex, and
is complex, and 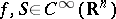 . If
. If 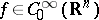 , i.e.
, i.e. 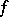 has compact support, and the phase
has compact support, and the phase 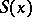 does not have stationary points (i.e. points at which
does not have stationary points (i.e. points at which 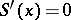 ) on
) on 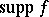 ,
, 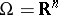 , then
, then 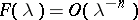 , for all
, for all  as
as 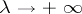 . Therefore, when
. Therefore, when 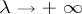 , the points of stationary phase and the boundary
, the points of stationary phase and the boundary 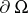 give the essential contribution to the asymptotics of the integral (*). The integrals
give the essential contribution to the asymptotics of the integral (*). The integrals
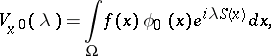 |
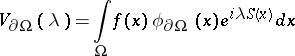 |
are called the contributions from the isolated stationary point 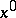 and the boundary, respectively, where
and the boundary, respectively, where 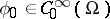 ,
, 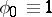 near the point
near the point 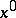 and
and 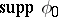 does not contain any other stationary points,
does not contain any other stationary points, 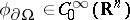 and
and 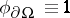 in a certain neighbourhood of the boundary. For
in a certain neighbourhood of the boundary. For 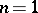 ,
, 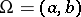 :
:
1) 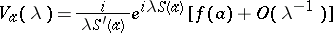 , if
, if 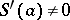 ;
;
2)
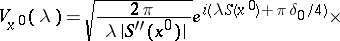 |
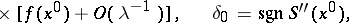 |
if 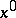 is an interior point of
is an interior point of  and
and 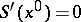 ,
, 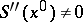 .
.
Detailed research has been carried out in the case where 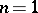 , the phase
, the phase 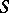 has a finite number of stationary points, all of finite multiplicity, and the function
has a finite number of stationary points, all of finite multiplicity, and the function 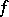 has zeros of finite multiplicity at these points and at the end-points of an interval
has zeros of finite multiplicity at these points and at the end-points of an interval  . Asymptotic expansions have been obtained. The case where the functions
. Asymptotic expansions have been obtained. The case where the functions 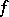 and
and 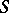 have power singularities has also been studied: for example,
have power singularities has also been studied: for example, 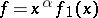 ,
, 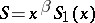 , where
, where 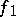 ,
, 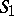 are smooth functions when
are smooth functions when 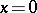 ,
, 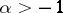 ,
, 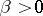 .
.
Let 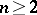 , and let
, and let 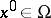 be a non-degenerate stationary point (i.e.
be a non-degenerate stationary point (i.e.  ). The contribution from the point
). The contribution from the point 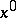 is then equal to
is then equal to
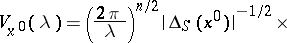 |
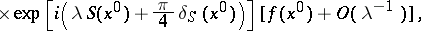 |
where 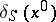 is the signature of the matrix
is the signature of the matrix 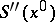 . There is also an asymptotic series for
. There is also an asymptotic series for 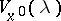 (for the formulas of the contribution
(for the formulas of the contribution 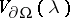 in the case of a smooth boundary, see [5]).
in the case of a smooth boundary, see [5]).
If 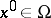 is a stationary point of finite multiplicity, then (see [6])
is a stationary point of finite multiplicity, then (see [6])
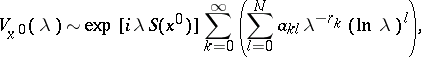 |
where 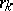 are rational numbers,
are rational numbers, 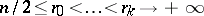 . Degenerate stationary points have been studied, cf. [3], [4].
. Degenerate stationary points have been studied, cf. [3], [4].
Studies have been made on the case where the phase 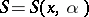 depends on a real parameter
depends on a real parameter 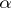 , and for small
, and for small 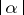 has two close non-degenerate stationary points. In this case, the asymptotics of the integral
has two close non-degenerate stationary points. In this case, the asymptotics of the integral 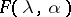 can be expressed in terms of Airy functions (see [5], [10]). The method of the stationary phase has an operator variant:
can be expressed in terms of Airy functions (see [5], [10]). The method of the stationary phase has an operator variant: 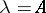 , where
, where 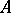 is the infinitesimal operator of the strongly-continuous group
is the infinitesimal operator of the strongly-continuous group 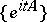 of operators bounded on the axis
of operators bounded on the axis 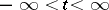 , acting on a Banach space
, acting on a Banach space 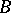 , and
, and 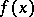 ,
, 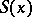 are smooth functions with values in
are smooth functions with values in 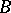 [9]. If the functions are analytic, then the method of the stationary phase is a particular case of the saddle point method.
[9]. If the functions are analytic, then the method of the stationary phase is a particular case of the saddle point method.
References
| [1] | W. Thomson, Philos. Mag. , 23 (1887) pp. 252–255 |
| [2] | A. Erdélyi, "Asymptotic expansions" , Dover, reprint (1956) MR0081379 MR0078494 Zbl 0072.11703 Zbl 0070.29002 |
| [3] | E.Ya. Rieksteyn'sh, "Asymptotic expansions of integrals" , 1–2 , Riga (1974–1977) (In Russian) |
| [4] | F.W.J. Olver, "Asymptotics and special functions" , Acad. Press (1974) MR0435697 Zbl 0308.41023 Zbl 0303.41035 |
| [5] | M.V. Fedoryuk, "The method of steepest descent" , Moscow (1977) (In Russian) |
| [6] | M.F. Atiyah, "Resolution of singularities and division of distributions" Comm. Pure Appl. Math. , 23 : 2 (1970) pp. 145–150 MR0256156 Zbl 0188.19405 |
| [7] | V.I. Arnol'd, "Remarks on the stationary phase method and Coxeter numbers" Russian Math. Surveys , 28 : 5 (1973) pp. 19–48 Uspekhi Mat. Nauk , 28 : 5 (1973) pp. 17–44 Zbl 0291.40005 |
| [8] | A.N. Varchenko, "Newton polyhedra and estimation of oscillating integrals" Funct. Anal. Appl , 10 : 3 (1976) pp. 175–196 Funktsional. Anal. i Prilozhen. , 10 : 3 (1976) pp. 13–38 Zbl 0351.32011 |
| [9] | V.P. Maslov, M.V. Fedoryuk, "Semi-classical approximation in quantum mechanics" , Reidel (1981) (Translated from Russian) Zbl 0458.58001 |
| [10] | M.V. Fedoryuk, "Asymptotics. Integrals and series" , Moscow (1987) (In Russian) MR0950167 Zbl 0641.41001 |
Comments
An integral of the form (*) is a special case of a so-called oscillatory integral, or Fourier integral operator, cf. also [a2].
References
| [a1] | R. Wong, "Asymptotic approximations of integrals" , Acad. Press (1989) MR1016818 Zbl 0679.41001 |
| [a2] | L.V. Hörmander, "The analysis of linear partial differential operators" , 1 , Springer (1983) pp. §7.7 MR0717035 MR0705278 Zbl 0521.35002 Zbl 0521.35001 |
Stationary phase, method of the. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Stationary_phase,_method_of_the&oldid=16013