Difference between revisions of "Zariski theorem"
(Importing text file) |
Ulf Rehmann (talk | contribs) m (MR/ZBL numbers added) |
||
| Line 6: | Line 6: | ||
====References==== | ====References==== | ||
| − | <table><TR><TD valign="top">[1]</TD> <TD valign="top"> | + | <table><TR><TD valign="top">[1]</TD> <TD valign="top"> O. Zariski, "Foundations of a general theory of birational correspondences" ''Trans. Amer. Math. Soc.'' , '''53''' : 3 (1943) pp. 490–542 {{MR|0008468}} {{ZBL|0061.33004}} </TD></TR><TR><TD valign="top">[2]</TD> <TD valign="top"> O. Zariski, "Theory and applications of holomorphic functions on algebraic varieties over arbitrary ground fields" ''Mem. Amer. Math. Soc.'' , '''5''' (1951) pp. 1–90 {{MR|0041487}} {{ZBL|}} </TD></TR><TR><TD valign="top">[3a]</TD> <TD valign="top"> A. Grothendieck, "Eléments de géometrie algébrique. III. Etude cohomologique des faisceaux cohérents I" ''Publ. Math. IHES'' , '''11''' (1961) {{MR|0217085}} {{MR|0163910}} {{ZBL|}} </TD></TR><TR><TD valign="top">[3b]</TD> <TD valign="top"> A. Grothendieck, "Eléments de géometrie algébrique. IV. Etude locale des schémas et des morphismes des schémas IV" ''Publ. Math. IHES'' , '''32''' (1967) {{MR|0238860}} {{ZBL|0144.19904}} {{ZBL|0135.39701}} {{ZBL|0136.15901}} </TD></TR></table> |
| Line 14: | Line 14: | ||
====References==== | ====References==== | ||
| − | <table><TR><TD valign="top">[a1]</TD> <TD valign="top"> | + | <table><TR><TD valign="top">[a1]</TD> <TD valign="top"> R. Hartshorne, "Algebraic geometry" , Springer (1977) pp. Sect. IV.2 {{MR|0463157}} {{ZBL|0367.14001}} </TD></TR><TR><TD valign="top">[a2]</TD> <TD valign="top"> O. Zariski, "The connectedness theorem for birational transformations" R.H. Fox (ed.) D.C. Spencer (ed.) A.W. Tucker (ed.) , ''Algebraic geometry and topology (Symp. in honor of S. Lefschetz)'' , Princeton Univ. Press (1957) pp. 182–188 {{MR|0090099}} {{ZBL|0087.35601}} </TD></TR><TR><TD valign="top">[a3]</TD> <TD valign="top"> J.P. Murre, "On a connectedness theorem for a birational transformation at a simple point" ''Amer. J. Math.'' , '''80''' (1958) pp. 3–15 {{MR|0093524}} {{ZBL|0087.35602}} </TD></TR><TR><TD valign="top">[a4]</TD> <TD valign="top"> W.-L. Chow, "On the connectedness theorem in algebraic geometry" ''Amer. J. Math.'' , '''83''' (1959) pp. 1033–1074 {{MR|0110705}} {{ZBL|0192.26806}} </TD></TR></table> |
Revision as of 21:57, 30 March 2012
on connectivity, Zariski connectedness theorem
Let  be a proper surjective morphism of irreducible varieties, let the field of rational functions
be a proper surjective morphism of irreducible varieties, let the field of rational functions  be separably algebraically closed in
be separably algebraically closed in  and let
and let  be a normal point; then
be a normal point; then  is connected (moreover, geometrically connected) (see [2]). The theorem provides a basis for the classical principle of degeneration: If the generic cycle of an algebraic system of cycles is a variety (i.e. is geometrically irreducible), then any specialization of that cycle is connected.
is connected (moreover, geometrically connected) (see [2]). The theorem provides a basis for the classical principle of degeneration: If the generic cycle of an algebraic system of cycles is a variety (i.e. is geometrically irreducible), then any specialization of that cycle is connected.
A special case of the Zariski connectedness theorem is the so-called fundamental theorem of Zariski, or Zariski's birational correspondence theorem: A birational morphism of algebraic varieties  is an open imbedding into a neighbourhood of a normal point
is an open imbedding into a neighbourhood of a normal point  if
if  is a finite set (see [1]). In particular, a birational morphism of normal varieties which is bijective at points is an isomorphism. Another formulation of this theorem: Let
is a finite set (see [1]). In particular, a birational morphism of normal varieties which is bijective at points is an isomorphism. Another formulation of this theorem: Let  be a quasi-finite separable morphism of schemes, and let
be a quasi-finite separable morphism of schemes, and let 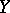 be a quasi-compact quasi-separable scheme; then there exists a decomposition
be a quasi-compact quasi-separable scheme; then there exists a decomposition  , where
, where  is a finite morphism and
is a finite morphism and  an open imbedding .
an open imbedding .
References
| [1] | O. Zariski, "Foundations of a general theory of birational correspondences" Trans. Amer. Math. Soc. , 53 : 3 (1943) pp. 490–542 MR0008468 Zbl 0061.33004 |
| [2] | O. Zariski, "Theory and applications of holomorphic functions on algebraic varieties over arbitrary ground fields" Mem. Amer. Math. Soc. , 5 (1951) pp. 1–90 MR0041487 |
| [3a] | A. Grothendieck, "Eléments de géometrie algébrique. III. Etude cohomologique des faisceaux cohérents I" Publ. Math. IHES , 11 (1961) MR0217085 MR0163910 |
| [3b] | A. Grothendieck, "Eléments de géometrie algébrique. IV. Etude locale des schémas et des morphismes des schémas IV" Publ. Math. IHES , 32 (1967) MR0238860 Zbl 0144.19904 Zbl 0135.39701 Zbl 0136.15901 |
Comments
In case 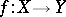 is a proper birational morphism and
is a proper birational morphism and  is a non-singular point,
is a non-singular point,  is moreover linearly connected, i.e. any two points of
is moreover linearly connected, i.e. any two points of  can be connected by a sequence of rational curves in
can be connected by a sequence of rational curves in  (see [a2]–[a4]).
(see [a2]–[a4]).
References
| [a1] | R. Hartshorne, "Algebraic geometry" , Springer (1977) pp. Sect. IV.2 MR0463157 Zbl 0367.14001 |
| [a2] | O. Zariski, "The connectedness theorem for birational transformations" R.H. Fox (ed.) D.C. Spencer (ed.) A.W. Tucker (ed.) , Algebraic geometry and topology (Symp. in honor of S. Lefschetz) , Princeton Univ. Press (1957) pp. 182–188 MR0090099 Zbl 0087.35601 |
| [a3] | J.P. Murre, "On a connectedness theorem for a birational transformation at a simple point" Amer. J. Math. , 80 (1958) pp. 3–15 MR0093524 Zbl 0087.35602 |
| [a4] | W.-L. Chow, "On the connectedness theorem in algebraic geometry" Amer. J. Math. , 83 (1959) pp. 1033–1074 MR0110705 Zbl 0192.26806 |
Zariski theorem. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Zariski_theorem&oldid=15861