Difference between revisions of "Form of an (algebraic) structure"
(Importing text file) |
Ulf Rehmann (talk | contribs) m (MR/ZBL numbers added) |
||
| Line 1: | Line 1: | ||
| − | Let <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f040/f040800/f0408001.png" /> be an extension of fields, and let <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f040/f040800/f0408002.png" /> be some | + | Let <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f040/f040800/f0408001.png" /> be an extension of fields, and let <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f040/f040800/f0408002.png" /> be some "object" defined over <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f040/f040800/f0408003.png" />. For example, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f040/f040800/f0408004.png" /> could be a vector space together with a quadratic form, a Lie algebra over <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f040/f040800/f0408005.png" />, an Azumaya algebra over <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f040/f040800/f0408006.png" />, a variety over <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f040/f040800/f0408007.png" />, an algebraic group over <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f040/f040800/f0408008.png" />, a representation of a finite group in a <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f040/f040800/f0408009.png" />-vector space, etc. A form of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f040/f040800/f04080010.png" /> over <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f040/f040800/f04080011.png" />, more precisely, a <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f040/f040800/f04080013.png" />-form, is an object <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f040/f040800/f04080014.png" /> of the same type over <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f040/f040800/f04080015.png" /> such that <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f040/f040800/f04080016.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f040/f040800/f04080017.png" /> become isomorphic over <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f040/f040800/f04080018.png" />, i.e. after extending scalars from <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f040/f040800/f04080019.png" /> to <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f040/f040800/f04080020.png" /> the objects <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f040/f040800/f04080021.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f040/f040800/f04080022.png" /> become isomorphic. Let <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f040/f040800/f04080023.png" /> denote the set of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f040/f040800/f04080024.png" />-isomorphism classes of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f040/f040800/f04080025.png" /> forms of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f040/f040800/f04080026.png" />. If now <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f040/f040800/f04080027.png" /> is a Galois extension, then under suitable circumstances one has a bijection between <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f040/f040800/f04080028.png" /> and the Galois cohomology group <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f040/f040800/f04080029.png" /> (cf. [[Galois cohomology|Galois cohomology]]), where <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f040/f040800/f04080030.png" /> is the group of automorphisms over <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f040/f040800/f04080031.png" /> of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f040/f040800/f04080032.png" />. Consider, for instance, the case where the object <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f040/f040800/f04080033.png" /> is a finite-dimensional algebra <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f040/f040800/f04080034.png" /> over <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f040/f040800/f04080035.png" />. Then <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f040/f040800/f04080036.png" /> is a form of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f040/f040800/f04080037.png" /> if <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f040/f040800/f04080038.png" /> as <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f040/f040800/f04080039.png" />-algebras. Let <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f040/f040800/f04080040.png" /> be an automorphism of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f040/f040800/f04080041.png" /> over <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f040/f040800/f04080042.png" />, i.e. an isomorphism of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f040/f040800/f04080043.png" />-algebras <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f040/f040800/f04080044.png" />, and let <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f040/f040800/f04080045.png" />. Then <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f040/f040800/f04080046.png" /> is another <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f040/f040800/f04080047.png" />-automorphism of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f040/f040800/f04080048.png" />. This defines the action of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f040/f040800/f04080049.png" /> on <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f040/f040800/f04080050.png" />. Now let <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f040/f040800/f04080051.png" /> be a form of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f040/f040800/f04080052.png" />. The set of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f040/f040800/f04080053.png" />-isomorphisms <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f040/f040800/f04080054.png" /> is naturally a principal homogeneous space over <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f040/f040800/f04080055.png" /> and thus defines an element of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f040/f040800/f04080056.png" />. This mapping is a bijection in this case. More generally one has such a bijection for the case that the structure <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f040/f040800/f04080057.png" /> is a vector space <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f040/f040800/f04080058.png" /> together with a <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f040/f040800/f04080059.png" />-tensor (the previous case corresponds to the case of a <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f040/f040800/f04080060.png" />-tensor). (To prove surjectivity one needs the generalization of Hilbert's theorem 90: <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f040/f040800/f04080061.png" />.) For the case of algebraic groups over <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f040/f040800/f04080062.png" /> cf. [[Form of an algebraic group|Form of an algebraic group]]. |
For the case of algebraic varieties over <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f040/f040800/f04080063.png" /> one has that <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f040/f040800/f04080064.png" /> is injective and that it is bijective if <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f040/f040800/f04080065.png" /> is quasi-projective. | For the case of algebraic varieties over <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f040/f040800/f04080063.png" /> one has that <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f040/f040800/f04080064.png" /> is injective and that it is bijective if <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f040/f040800/f04080065.png" /> is quasi-projective. | ||
| Line 40: | Line 40: | ||
====References==== | ====References==== | ||
| − | <table><TR><TD valign="top">[a1]</TD> <TD valign="top"> | + | <table><TR><TD valign="top">[a1]</TD> <TD valign="top"> M.-A. Knus, M. Ojanguren, "Théorie de la descent et algèbres d'Azumaya" , Springer (1974) {{MR|417149}} {{ZBL|}} </TD></TR><TR><TD valign="top">[a2]</TD> <TD valign="top"> A. Grothendieck, "Revêtements étales et groupe fondamental" , ''SGA 1960–1961'' , '''Exp. VI: Categories fibrées et descente''' , IHES (1961) {{MR|2017446}} {{MR|0354651}} {{MR|0217088}} {{MR|0217087}} {{ZBL|1039.14001}} </TD></TR><TR><TD valign="top">[a3]</TD> <TD valign="top"> J.P. Murre, "Lectures on an introduction to Grothendieck's theory of the fundamental group." , Tata Inst. Fund. Res. (1967) pp. Chapt. VII {{MR|302650}} {{ZBL|}} </TD></TR><TR><TD valign="top">[a4]</TD> <TD valign="top"> J.-P. Serre, "Cohomologie Galoisienne" , Springer (1973) {{MR|0404227}} {{ZBL|0259.12011}} </TD></TR><TR><TD valign="top">[a5]</TD> <TD valign="top"> G.B. Seligman, "Modular Lie algebras" , Springer (1967) pp. Chapt. IV {{MR|0245627}} {{ZBL|0189.03201}} </TD></TR><TR><TD valign="top">[a6]</TD> <TD valign="top"> J.-P. Serre, "Groupes algébrique et corps des classes" , Hermann (1959) pp. Chapt. V, Sect. 20 {{MR|0103191}} {{ZBL|}} </TD></TR><TR><TD valign="top">[a7]</TD> <TD valign="top"> N. Jacobson, "Lie algebras" , Dover, reprint (1979) pp. Chapt. X ((also: Dover, reprint, 1979)) {{MR|0559927}} {{ZBL|0333.17009}} {{ZBL|0215.38701}} {{ZBL|0144.27103}} {{ZBL|0121.27601}} {{ZBL|0121.27504}} {{ZBL|0109.26201}} {{ZBL|0198.05404}} {{ZBL|0064.27002}} {{ZBL|0064.03503}} {{ZBL|0046.03402}} {{ZBL|0043.26803}} {{ZBL|0039.02803}} {{ZBL|0063.03015}} {{ZBL|0025.30302}} {{ZBL|0025.30301}} {{ZBL|0022.19801}} {{ZBL|0019.19402}} {{ZBL|0018.10302}} {{ZBL|0017.29203}} {{ZBL|0016.20001}} </TD></TR></table> |
Revision as of 14:49, 24 March 2012
Let 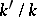 be an extension of fields, and let
be an extension of fields, and let 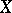 be some "object" defined over
be some "object" defined over 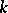 . For example,
. For example, 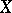 could be a vector space together with a quadratic form, a Lie algebra over
could be a vector space together with a quadratic form, a Lie algebra over 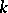 , an Azumaya algebra over
, an Azumaya algebra over 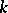 , a variety over
, a variety over 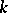 , an algebraic group over
, an algebraic group over 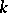 , a representation of a finite group in a
, a representation of a finite group in a 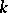 -vector space, etc. A form of
-vector space, etc. A form of 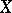 over
over 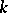 , more precisely, a
, more precisely, a 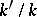 -form, is an object
-form, is an object 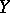 of the same type over
of the same type over 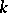 such that
such that 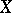 and
and 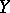 become isomorphic over
become isomorphic over 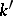 , i.e. after extending scalars from
, i.e. after extending scalars from 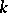 to
to 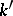 the objects
the objects 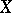 and
and 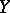 become isomorphic. Let
become isomorphic. Let 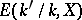 denote the set of
denote the set of 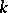 -isomorphism classes of
-isomorphism classes of  forms of
forms of 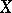 . If now
. If now 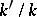 is a Galois extension, then under suitable circumstances one has a bijection between
is a Galois extension, then under suitable circumstances one has a bijection between 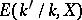 and the Galois cohomology group
and the Galois cohomology group 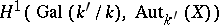 (cf. Galois cohomology), where
(cf. Galois cohomology), where 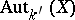 is the group of automorphisms over
is the group of automorphisms over 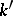 of
of 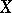 . Consider, for instance, the case where the object
. Consider, for instance, the case where the object 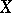 is a finite-dimensional algebra
is a finite-dimensional algebra 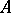 over
over 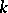 . Then
. Then 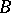 is a form of
is a form of 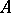 if
if 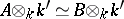 as
as 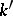 -algebras. Let
-algebras. Let 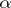 be an automorphism of
be an automorphism of 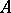 over
over 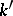 , i.e. an isomorphism of
, i.e. an isomorphism of 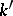 -algebras
-algebras 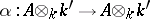 , and let
, and let 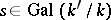 . Then
. Then 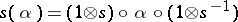 is another
is another 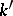 -automorphism of
-automorphism of 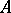 . This defines the action of
. This defines the action of 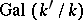 on
on 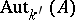 . Now let
. Now let 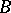 be a form of
be a form of 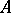 . The set of
. The set of 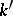 -isomorphisms
-isomorphisms 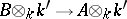 is naturally a principal homogeneous space over
is naturally a principal homogeneous space over 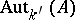 and thus defines an element of
and thus defines an element of 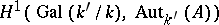 . This mapping is a bijection in this case. More generally one has such a bijection for the case that the structure
. This mapping is a bijection in this case. More generally one has such a bijection for the case that the structure 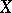 is a vector space
is a vector space 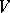 together with a
together with a 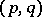 -tensor (the previous case corresponds to the case of a
-tensor (the previous case corresponds to the case of a 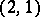 -tensor). (To prove surjectivity one needs the generalization of Hilbert's theorem 90:
-tensor). (To prove surjectivity one needs the generalization of Hilbert's theorem 90: 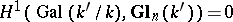 .) For the case of algebraic groups over
.) For the case of algebraic groups over 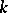 cf. Form of an algebraic group.
cf. Form of an algebraic group.
For the case of algebraic varieties over 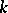 one has that
one has that 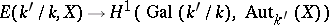 is injective and that it is bijective if
is injective and that it is bijective if 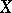 is quasi-projective.
is quasi-projective.
The concept of forms makes sense in a far more general setting, e.g. in any category with base change, i.e. with fibre products. Indeed, let 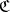 be such a category, and
be such a category, and 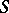 an object in
an object in 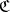 . An object over
. An object over 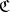 is a morphism in
is a morphism in 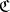 ,
, 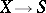 . Let
. Let 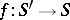 be a morphism in
be a morphism in 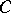 . Base change from
. Base change from 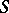 to
to 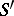 gives the pullback (fibre product)
gives the pullback (fibre product) 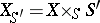 defined by the Cartesian square
defined by the Cartesian square
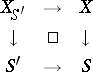 |
(In case 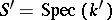 ,
, 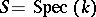 and
and 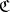 is, for instance, the category of (affine) schemes this corresponds to extending scalars.)
is, for instance, the category of (affine) schemes this corresponds to extending scalars.)
An object 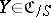 is now an
is now an  -form of
-form of 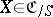 if the objects
if the objects 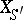 and
and 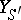 are isomorphic over
are isomorphic over 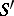 . For an even more general setting cf. [a2].
. For an even more general setting cf. [a2].
A related problem (to that of forms) is the subject of descent theory. In the setting of a category with base change as above this theory is concerned with the question: Given 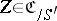 , does there exists an
, does there exists an 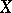 over
over 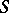 such that
such that 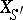 is isomorphic over
is isomorphic over 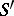 to
to 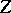 , and what properties must
, and what properties must 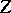 satisfy for this to be the case.
satisfy for this to be the case.
Below this question is examined in the following setting: 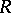 is a commutative algebra (with unit element) and
is a commutative algebra (with unit element) and 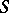 is a commutative
is a commutative 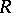 -algebra. Given a module
-algebra. Given a module 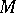 over
over 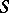 the question is whether there exists a module
the question is whether there exists a module 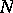 over
over 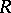 such that
such that 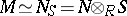 (as
(as 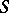 -modules). Below all tensor products
-modules). Below all tensor products 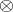 are tensor products over
are tensor products over 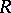 :
: 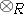 . If
. If  is of the form
is of the form 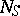 there is a natural isomorphism of
there is a natural isomorphism of  modules
modules 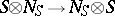 given by
given by 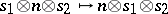 . Let
. Let 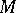 be an
be an 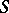 -module. A descent datum on
-module. A descent datum on 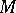 is an isomorphism of
is an isomorphism of  modules
modules 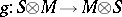 such that
such that 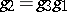 . Here
. Here 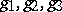 are the three natural
are the three natural 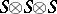 -module homomorphisms defined by
-module homomorphisms defined by 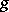 , where
, where 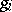 is the identity on factor
is the identity on factor 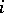 and given by
and given by 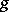 on the other two components:
on the other two components:
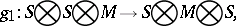 |
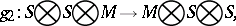 |
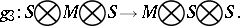 |
The faithfully flat descent theorem now says that if 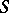 is faithfully flat over
is faithfully flat over 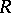 and
and 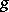 is a descent datum for
is a descent datum for 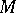 over
over 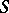 , then there exists an
, then there exists an 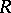 -module
-module 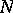 and an isomorphism
and an isomorphism 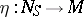 such that the following diagram commutes
such that the following diagram commutes
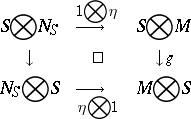 |
where the left vertical arrow is the descent datum on 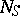 described above. Moreover, the pair
described above. Moreover, the pair 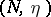 is uniquely defined by this property. One defines
is uniquely defined by this property. One defines 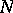 by an invariance property:
by an invariance property: 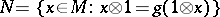 (which is like invariance under the Galois group in the case of Galois descent).
(which is like invariance under the Galois group in the case of Galois descent).
There is a similar theorem for descent of algebras over 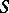 .
.
In algebraic geometry one has for instance the following descent theorem (a globalization of the previous one for algebras). For a morphism of schemes 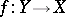 , consider the fibre products
, consider the fibre products 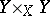 and
and 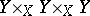 and let
and let 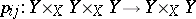 be the projections
be the projections 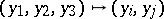 ,
, 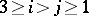 ; and
; and 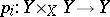 the projections
the projections 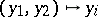 ,
, 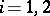 . Let
. Let 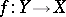 be faithfully flat and compact. Then to give a scheme
be faithfully flat and compact. Then to give a scheme 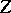 affine over
affine over 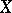 is the same as to give a scheme
is the same as to give a scheme 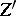 affine over
affine over 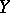 together with an isomorphism
together with an isomorphism 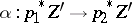 such that
such that 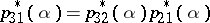 .
.
The theory of descent is quite general and includes such matters as specifying a section of a sheaf by local sections and the construction of locally trivial fibre bundles by glueing together trivial bundles 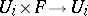 over the elements of an open covering
over the elements of an open covering 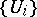 of
of 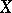 . Indeed, let
. Indeed, let 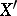 be the disjoint union of the
be the disjoint union of the 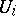 and
and 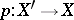 the natural projection. Giving glueing data
the natural projection. Giving glueing data 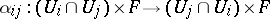 is the same as giving an isomorphism
is the same as giving an isomorphism 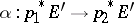 , where
, where 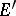 is the trivial vector bundle
is the trivial vector bundle 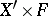 with fibre
with fibre 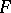 and the compatibility of the glueing data amounts to the condition
and the compatibility of the glueing data amounts to the condition 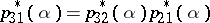 .
.
For a treatment of forms of Lie algebras (over fields) cf. [a7], for Lie algebras over characteristic zero fields and the modular case (i.e. over fields of characteristic 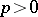 ) cf. [a5]. For a quite comprehensive treatment of descent and forms cf. [a1].
) cf. [a5]. For a quite comprehensive treatment of descent and forms cf. [a1].
A form of an object is also occasionally called a twisted form.
In the case of descent with respect to a Galois field extension 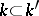 (or
(or 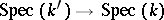 ) one speaks of Galois descent.
) one speaks of Galois descent.
References
| [a1] | M.-A. Knus, M. Ojanguren, "Théorie de la descent et algèbres d'Azumaya" , Springer (1974) MR417149 |
| [a2] | A. Grothendieck, "Revêtements étales et groupe fondamental" , SGA 1960–1961 , Exp. VI: Categories fibrées et descente , IHES (1961) MR2017446 MR0354651 MR0217088 MR0217087 Zbl 1039.14001 |
| [a3] | J.P. Murre, "Lectures on an introduction to Grothendieck's theory of the fundamental group." , Tata Inst. Fund. Res. (1967) pp. Chapt. VII MR302650 |
| [a4] | J.-P. Serre, "Cohomologie Galoisienne" , Springer (1973) MR0404227 Zbl 0259.12011 |
| [a5] | G.B. Seligman, "Modular Lie algebras" , Springer (1967) pp. Chapt. IV MR0245627 Zbl 0189.03201 |
| [a6] | J.-P. Serre, "Groupes algébrique et corps des classes" , Hermann (1959) pp. Chapt. V, Sect. 20 MR0103191 |
| [a7] | N. Jacobson, "Lie algebras" , Dover, reprint (1979) pp. Chapt. X ((also: Dover, reprint, 1979)) MR0559927 Zbl 0333.17009 Zbl 0215.38701 Zbl 0144.27103 Zbl 0121.27601 Zbl 0121.27504 Zbl 0109.26201 Zbl 0198.05404 Zbl 0064.27002 Zbl 0064.03503 Zbl 0046.03402 Zbl 0043.26803 Zbl 0039.02803 Zbl 0063.03015 Zbl 0025.30302 Zbl 0025.30301 Zbl 0022.19801 Zbl 0019.19402 Zbl 0018.10302 Zbl 0017.29203 Zbl 0016.20001 |
Form of an (algebraic) structure. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Form_of_an_(algebraic)_structure&oldid=15826