Difference between revisions of "Jordan-Dedekind space"
(Importing text file) |
Ulf Rehmann (talk | contribs) m (moved Jordan–Dedekind space to Jordan-Dedekind space: ascii title) |
(No difference)
| |
Revision as of 18:52, 24 March 2012
Let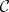 
be a closure space on a set 
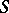. The elements of 
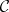, partially ordered by set-inclusion, form a complete atomic lattice [a3] (cf. also Atom). For any subset 
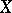of 
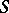, let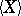 
denote the closure of 
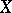. A chain in a closed set 
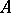is a totally ordered set of closed subsets of 
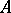. The rank 
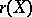of a set 
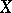is
 |
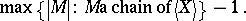A Jordan–Dedekind space is a closure space of finite rank satisfying the Jordan–Dedekind chain condition (see Jordan–Dedekind lattice).
Characterizations of Jordan–Dedekind spaces in terms of an exchange property and in terms of independence were given by L.M. Batten in [a1] and [a2]. In particular, let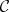 
be a closure space. 
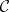is said to have the weak exchange property if for all elements 
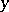of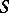 
and subsets 
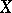of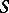 
,
 |
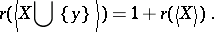The following theorem holds: In any closure space of finite rank, the weak exchange property is equivalent to the Jordan–Dedekind chain condition (cf. Jordan–Dedekind property).
The notion of an independent set is recursively defined: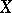 
is independent if 
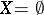or a singleton; 
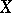is independent if for some 
, 
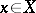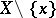is independent and 
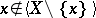. The set 
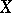is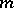 
-independent if for all 
, 
.
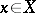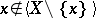The following theorem holds: For a Jordan–Dedekind space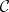 
the following assertions are equivalent: 1) 
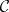is a matroid [a4]; and 2) 
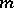-independence and independence are the same.
References
| [a1] | L.M. Batten, "A rank-associated notion of independence" , Finite Geometries , M. Dekker (1983) |
| [a2] | L.M. Batten, "Jordan–Dedekind spaces" Quart. J. Math. Oxford , 35 (1984) pp. 373–381 |
| [a3] | G. Birkhoff, "Lattice theory" , Colloq. Publ. , Amer. Math. Soc. (1967) (Edition: Third) |
| [a4] | D.J.A. Welsh, "Matroid theory" , Acad. Press (1976) |
Jordan-Dedekind space. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Jordan-Dedekind_space&oldid=15264