Difference between revisions of "Taylor joint spectrum"
(Importing text file) |
Ulf Rehmann (talk | contribs) m (MR/ZBL numbers added) |
||
| Line 31: | Line 31: | ||
so <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t130/t130050/t13005073.png" />. | so <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t130/t130050/t13005073.png" />. | ||
| − | Note that since <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t130/t130050/t13005074.png" /> is defined in terms of the actions of the operators <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t130/t130050/t13005075.png" /> on vectors of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t130/t130050/t13005076.png" />, it is intrinsically | + | Note that since <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t130/t130050/t13005074.png" /> is defined in terms of the actions of the operators <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t130/t130050/t13005075.png" /> on vectors of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t130/t130050/t13005076.png" />, it is intrinsically "spatial" , as opposed to <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t130/t130050/t13005077.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t130/t130050/t13005078.png" /> and other algebraic joint spectra. <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t130/t130050/t13005079.png" /> contains other well-known spatial spectra, like <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t130/t130050/t13005080.png" /> (the point spectrum), <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t130/t130050/t13005081.png" /> (the approximate point spectrum) and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t130/t130050/t13005082.png" /> (the defect spectrum). Moreover, if <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t130/t130050/t13005083.png" /> is a commutative Banach algebra, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t130/t130050/t13005084.png" />, with each <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t130/t130050/t13005085.png" />, and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t130/t130050/t13005086.png" /> denotes the <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t130/t130050/t13005087.png" />-tuple of left multiplications by the <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t130/t130050/t13005088.png" />s, it is not hard to show that <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t130/t130050/t13005089.png" />. As a matter of fact, the same result holds when <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t130/t130050/t13005090.png" /> is not commutative, provided all the <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t130/t130050/t13005091.png" />s come from the centre of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t130/t130050/t13005092.png" />. |
===Spectral permanence.=== | ===Spectral permanence.=== | ||
| Line 94: | Line 94: | ||
<table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t130/t130050/t130050182.png" /></td> </tr></table> | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t130/t130050/t130050182.png" /></td> </tr></table> | ||
| − | During the 1980s and 1990s, Taylor spectral theory has received considerable attention; for further details and information, see [[#References|[a2]]], [[#References|[a11]]], [[#References|[a20]]], [[#References|[a10]]], [[#References|[a1]]]. There is also a parallel | + | During the 1980s and 1990s, Taylor spectral theory has received considerable attention; for further details and information, see [[#References|[a2]]], [[#References|[a11]]], [[#References|[a20]]], [[#References|[a10]]], [[#References|[a1]]]. There is also a parallel "local spectral theory" , described in [[#References|[a11]]], [[#References|[a12]]] and [[#References|[a20]]]. |
====References==== | ====References==== | ||
| − | <table><TR><TD valign="top">[a1]</TD> <TD valign="top"> | + | <table><TR><TD valign="top">[a1]</TD> <TD valign="top"> E. Albrecht, F.-H. Vasilescu, "Semi-Fredholm complexes" ''Oper. Th. Adv. Appl.'' , '''11''' (1983) pp. 15–39 {{MR|0789629}} {{ZBL|0527.47008}} </TD></TR><TR><TD valign="top">[a2]</TD> <TD valign="top"> C.-G. Ambrozie, F.-H. Vasilescu, "Banach space complexes" , Kluwer Acad. Publ. (1995) {{MR|1357165}} {{ZBL|0837.47009}} </TD></TR><TR><TD valign="top">[a3]</TD> <TD valign="top"> C. Berger, L. Coburn, A. Koranyi, "Opérateurs de Wiener–Hopf sur les spheres de Lie" ''C.R. Acad. Sci. Paris Sér. A'' , '''290''' (1980) pp. 989–991 {{MR|584284}} {{ZBL|0436.47021}} </TD></TR><TR><TD valign="top">[a4]</TD> <TD valign="top"> C. Berger, L. Coburn, "Wiener–Hopf operators on <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t130/t130050/t130050183.png" />" ''Integral Eq. Oper. Th.'' , '''2''' (1979) pp. 139–173 {{MR|0543881}} {{ZBL|0434.47019}} </TD></TR><TR><TD valign="top">[a5]</TD> <TD valign="top"> R. Curto, L. Fialkow, "The spectral picture of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t130/t130050/t130050184.png" />" ''J. Funct. Anal.'' , '''71''' (1987) pp. 371–392 {{MR|0880986}} {{ZBL|0626.47018}} </TD></TR><TR><TD valign="top">[a6]</TD> <TD valign="top"> R. Curto, P. Muhly, "<img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t130/t130050/t130050185.png" />-algebras of multiplication operators on Bergman spaces" ''J. Funct. Anal.'' , '''64''' (1985) pp. 315–329 {{MR|0813203}} {{ZBL|0583.46049}} </TD></TR><TR><TD valign="top">[a7]</TD> <TD valign="top"> R. Curto, N. Salinas, "Spectral properties of cyclic subnormal <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t130/t130050/t130050186.png" />-tuples" ''Amer. J. Math.'' , '''107''' (1985) pp. 113–138 {{MR|778091}} {{ZBL|}} </TD></TR><TR><TD valign="top">[a8]</TD> <TD valign="top"> R. Curto, K. Yan, "The spectral picture of Reinhardt measures" ''J. Funct. Anal.'' , '''131''' (1995) pp. 279–301 {{MR|1345033}} {{ZBL|0826.47002}} </TD></TR><TR><TD valign="top">[a9]</TD> <TD valign="top"> R. Curto, "Spectral permanence for joint spectra" ''Trans. Amer. Math. Soc.'' , '''270''' (1982) pp. 659–665 {{MR|0645336}} {{ZBL|0508.47039}} {{ZBL|0491.47020}} </TD></TR><TR><TD valign="top">[a10]</TD> <TD valign="top"> R. Curto, "Applications of several complex variables to multiparameter spectral theory" J.B. Conway (ed.) B.B. Morrel (ed.) , ''Surveys of Some Recent Results in Operator Theory II'' , ''Pitman Res. Notes in Math.'' , '''192''' , Longman Sci. Tech. (1988) pp. 25–90 {{MR|0976843}} {{ZBL|0827.47005}} </TD></TR><TR><TD valign="top">[a11]</TD> <TD valign="top"> J. Eschmeier, M. Putinar, "Spectral decompositions and analytic sheaves" , ''London Math. Soc. Monographs'' , Oxford Sci. Publ. (1996) {{MR|1420618}} {{ZBL|0855.47013}} </TD></TR><TR><TD valign="top">[a12]</TD> <TD valign="top"> K. Laursen, M. Neumann, "Introduction to local spectral theory" , ''London Math. Soc. Monographs'' , Oxford Univ. Press (2000) {{MR|1747914}} {{ZBL|0957.47004}} </TD></TR><TR><TD valign="top">[a13]</TD> <TD valign="top"> M. Putinar, "Uniqueness of Taylor's functional calculus" ''Proc. Amer. Math. Soc.'' , '''89''' (1983) pp. 647–650 {{MR|718990}} {{ZBL|}} </TD></TR><TR><TD valign="top">[a14]</TD> <TD valign="top"> M. Putinar, "Spectral inclusion for subnormal <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t130/t130050/t130050187.png" />-tuples" ''Proc. Amer. Math. Soc.'' , '''90''' (1984) pp. 405–406 {{MR|728357}} {{ZBL|}} </TD></TR><TR><TD valign="top">[a15]</TD> <TD valign="top"> N. Salinas, A. Sheu, H. Upmeier, "Toeplitz operators on pseudoconvex domains and foliation <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t130/t130050/t130050188.png" />-algebras" ''Ann. of Math.'' , '''130''' (1989) pp. 531–565 {{MR|1025166}} {{ZBL|}} </TD></TR><TR><TD valign="top">[a16]</TD> <TD valign="top"> N. Salinas, "The <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t130/t130050/t130050189.png" />-formalism and the <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t130/t130050/t130050190.png" />-algebra of the Bergman <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t130/t130050/t130050191.png" />-tuple" ''J. Oper. Th.'' , '''22''' (1989) pp. 325–343 {{MR|1043731}} {{ZBL|}} </TD></TR><TR><TD valign="top">[a17]</TD> <TD valign="top"> J.L. Taylor, "A joint spectrum for several commuting operators" ''J. Funct. Anal.'' , '''6''' (1970) pp. 172–191 {{MR|0268706}} {{ZBL|0233.47024}} </TD></TR><TR><TD valign="top">[a18]</TD> <TD valign="top"> J.L. Taylor, "The analytic functional calculus for several commuting operators" ''Acta Math.'' , '''125''' (1970) pp. 1–48 {{MR|0271741}} {{ZBL|0233.47025}} </TD></TR><TR><TD valign="top">[a19]</TD> <TD valign="top"> H. Upmeier, "Toeplitz <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t130/t130050/t130050192.png" />-algebras on bounded symmetric domains" ''Ann. of Math.'' , '''119''' (1984) pp. 549–576 {{MR|744863}} {{ZBL|}} </TD></TR><TR><TD valign="top">[a20]</TD> <TD valign="top"> F.-H. Vasilescu, "Analytic functional calculus and spectral decompositions" , Reidel (1982) {{MR|0690957}} {{ZBL|0495.47013}} </TD></TR><TR><TD valign="top">[a21]</TD> <TD valign="top"> U. Venugopalkrishna, "Fredholm operators associated with strongly pseudoconvex domains in <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t130/t130050/t130050193.png" />" ''J. Funct. Anal.'' , '''9''' (1972) pp. 349–373 {{MR|0315502}} {{ZBL|0241.47023}} </TD></TR></table> |
Revision as of 17:02, 15 April 2012
Let 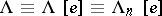 be the exterior algebra on
be the exterior algebra on  generators
generators  , with identity
, with identity 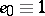 .
. 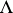 is the algebra of forms in
is the algebra of forms in  with complex coefficients, subject to the collapsing property
with complex coefficients, subject to the collapsing property 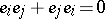 (
(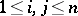 ). Let
). Let 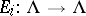 denote the creation operator, given by
denote the creation operator, given by 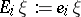 (
(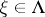 ,
, 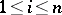 ). If one declares
). If one declares 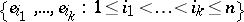 to be an orthonormal basis, the exterior algebra
to be an orthonormal basis, the exterior algebra 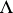 becomes a Hilbert space, admitting an orthogonal decomposition
becomes a Hilbert space, admitting an orthogonal decomposition 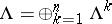 , where
, where 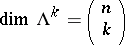 . Thus, each
. Thus, each 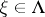 admits a unique orthogonal decomposition
admits a unique orthogonal decomposition 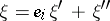 , where
, where 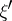 and
and 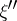 have no
have no 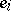 contribution. It then readily follows that
contribution. It then readily follows that 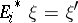 . Indeed, each
. Indeed, each 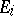 is a partial isometry, satisfying
is a partial isometry, satisfying 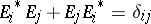 (
(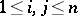 ).
).
Let 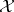 be a normed space, let
be a normed space, let 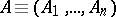 be a commuting
be a commuting  -tuple of bounded operators on
-tuple of bounded operators on 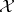 and set
and set  . One defines
. One defines 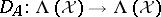 by
by 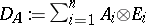 . Clearly,
. Clearly, 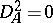 , so
, so 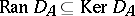 .
.
The commuting  -tuple
-tuple  is said to be non-singular on
is said to be non-singular on 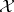 if
if 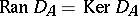 . The Taylor joint spectrum, or simply the Taylor spectrum, of
. The Taylor joint spectrum, or simply the Taylor spectrum, of 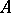 on
on 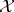 is the set
is the set
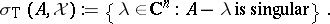 |
The decomposition 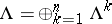 gives rise to a cochain complex
gives rise to a cochain complex 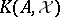 , the so-called Koszul complex associated to
, the so-called Koszul complex associated to  on
on 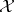 , as follows:
, as follows:
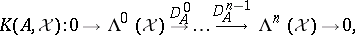 |
where 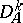 denotes the restriction of
denotes the restriction of 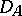 to the subspace
to the subspace 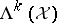 . Thus,
. Thus,
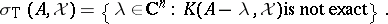 |
J.L. Taylor showed in [a17] that if 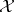 is a Banach space, then
is a Banach space, then 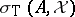 is compact, non-empty, and contained in
is compact, non-empty, and contained in 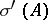 , the (joint) algebraic spectrum of
, the (joint) algebraic spectrum of 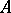 (cf. also Spectrum of an operator) with respect to the commutant of
(cf. also Spectrum of an operator) with respect to the commutant of 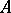 ,
, 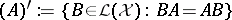 . Moreover,
. Moreover, 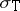 carries an analytic functional calculus with values in the double commutant of
carries an analytic functional calculus with values in the double commutant of 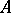 , so that, in particular,
, so that, in particular, 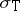 possesses the projection property.
possesses the projection property.
Example: 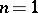 .
.
For 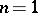 ,
, 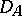 admits the following
admits the following 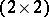 -matrix relative to the direct sum decomposition
-matrix relative to the direct sum decomposition 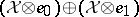 :
:
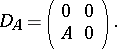 |
Then 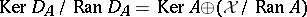 . It follows at once that
. It follows at once that 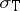 agrees with
agrees with  , the spectrum of
, the spectrum of  .
.
Example: 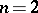 .
.
For 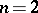 ,
,
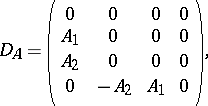 |
so 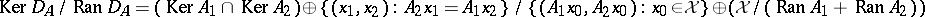 .
.
Note that since 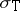 is defined in terms of the actions of the operators
is defined in terms of the actions of the operators 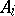 on vectors of
on vectors of 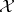 , it is intrinsically "spatial" , as opposed to
, it is intrinsically "spatial" , as opposed to  ,
, 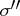 and other algebraic joint spectra.
and other algebraic joint spectra. 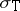 contains other well-known spatial spectra, like
contains other well-known spatial spectra, like 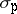 (the point spectrum),
(the point spectrum), 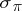 (the approximate point spectrum) and
(the approximate point spectrum) and 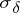 (the defect spectrum). Moreover, if
(the defect spectrum). Moreover, if 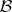 is a commutative Banach algebra,
is a commutative Banach algebra, 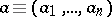 , with each
, with each 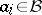 , and
, and 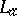 denotes the
denotes the  -tuple of left multiplications by the
-tuple of left multiplications by the 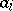 s, it is not hard to show that
s, it is not hard to show that 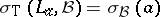 . As a matter of fact, the same result holds when
. As a matter of fact, the same result holds when 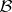 is not commutative, provided all the
is not commutative, provided all the 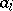 s come from the centre of
s come from the centre of 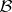 .
.
Spectral permanence.
When 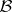 is a
is a 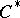 -algebra, say
-algebra, say 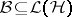 , then
, then  [a9]. This fact, known as spectral permanence for the Taylor spectrum, shows that for
[a9]. This fact, known as spectral permanence for the Taylor spectrum, shows that for 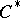 -algebra elements (and also for Hilbert space operators), the non-singularity of
-algebra elements (and also for Hilbert space operators), the non-singularity of 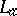 is equivalent to the invertibility of the associated Dirac operator
is equivalent to the invertibility of the associated Dirac operator 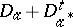 .
.
Finite-dimensional case.
When 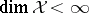 ,
,
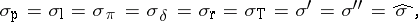 |
where 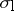 ,
, 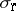 and
and 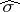 denote the left, right and polynomially convex spectra, respectively. As a matter of fact, in this case the commuting
denote the left, right and polynomially convex spectra, respectively. As a matter of fact, in this case the commuting  -tuple
-tuple 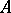 can be simultaneously triangularized as
can be simultaneously triangularized as 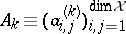 , and
, and
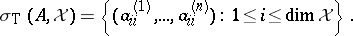 |
Case of compact operators.
If 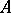 is a commuting
is a commuting  -tuple of compact operators acting on a Banach space
-tuple of compact operators acting on a Banach space 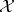 , then
, then 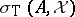 is countable, with
is countable, with 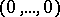 as the only accumulation point. Moreover,
as the only accumulation point. Moreover, 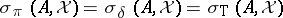 .
.
Invariant subspaces.
If 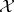 is a Banach space,
is a Banach space, 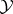 is a closed subspace of
is a closed subspace of 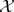 and
and 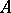 is a commuting
is a commuting  -tuple leaving
-tuple leaving 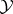 invariant, then the union of any two of the sets
invariant, then the union of any two of the sets  ,
, 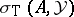 and
and 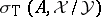 contains the third [a17]. This can be seen by looking at the long cohomology sequence associated to the Koszul complex and the canonical short exact sequence
contains the third [a17]. This can be seen by looking at the long cohomology sequence associated to the Koszul complex and the canonical short exact sequence  .
.
Additional properties.
In addition to the above-mentioned properties of 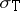 , the following facts can be found in the survey article [a10] and the references therein:
, the following facts can be found in the survey article [a10] and the references therein:
i) 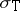 gives rise to a compact non-empty subset
gives rise to a compact non-empty subset 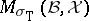 of the maximal ideal space of any commutative Banach algebra
of the maximal ideal space of any commutative Banach algebra 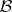 containing
containing 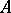 , in such a way that
, in such a way that 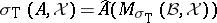 [a17];
[a17];
ii) for 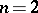 ,
, 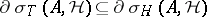 , where
, where 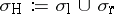 denotes the Harte spectrum;
denotes the Harte spectrum;
iii) the upper semi-continuity of separate parts holds for the Taylor spectrum;
iv) every isolated point in 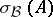 is an isolated point of
is an isolated point of 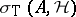 (and, a fortiori, an isolated point of
(and, a fortiori, an isolated point of 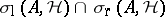 );
);
v) if 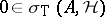 , up to approximate unitary equivalence one can always assume that
, up to approximate unitary equivalence one can always assume that  [a5];
[a5];
vi) the functional calculus introduced by Taylor in [a18] admits a concrete realization in terms of the Bochner–Martinelli kernel (cf. Bochner–Martinelli representation formula) in case 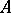 acts on a Hilbert space or on a
acts on a Hilbert space or on a 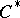 -algebra [a20];
-algebra [a20];
vii) M. Putinar established in [a13] the uniqueness of the functional calculus, provided it extends the polynomial calculus.
Fredholm  -tuples.
-tuples.
In a way entirely similar to the development of Fredholm theory, one can define the notion of Fredholm  -tuple: a commuting
-tuple: a commuting  -tuple
-tuple 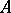 is said to be Fredholm on
is said to be Fredholm on 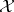 if the associated Koszul complex
if the associated Koszul complex 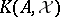 has finite-dimensional cohomology spaces. The Taylor essential spectrum of
has finite-dimensional cohomology spaces. The Taylor essential spectrum of 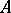 on
on 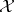 is then
is then
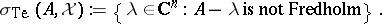 |
The Fredholm index of 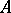 is defined as the Euler characteristic of
is defined as the Euler characteristic of 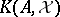 . For example, if
. For example, if 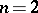 ,
, 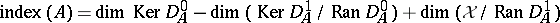 . In a Hilbert space,
. In a Hilbert space, 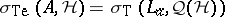 , where
, where 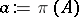 is the coset of
is the coset of 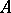 in the Calkin algebra for
in the Calkin algebra for 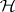 .
.
Example.
If 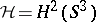 and
and 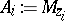 (
(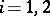 ), then
), then 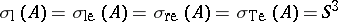 ,
, 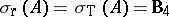 , and
, and 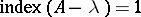 (
( ).
).
The Taylor spectral and Fredholm theories of multiplication operators acting on Bergman spaces over Reinhardt domains or bounded pseudo-convex domains, or acting on the Hardy spaces over the Shilov boundary of bounded symmetric domains on several complex variables, have been described in [a4], [a3], [a6], [a7], [a8], [a16], [a15], [a19], and [a21]; for Toeplitz operators with 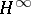 symbols acting on bounded pseudo-convex domains, concrete descriptions appear in [a11].
symbols acting on bounded pseudo-convex domains, concrete descriptions appear in [a11].
Spectral inclusion.
If 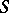 is a subnormal
is a subnormal  -tuple acting on
-tuple acting on 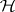 with minimal normal extension
with minimal normal extension 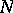 acting on
acting on 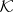 (cf. also Normal operator),
(cf. also Normal operator), 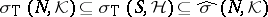 [a14].
[a14].
Left and right multiplications.
For 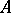 and
and  two commuting
two commuting  -tuples of operators on a Hilbert space
-tuples of operators on a Hilbert space 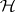 , and
, and 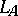 and
and 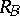 the associated
the associated  -tuples of left and right multiplication operators [a5],
-tuples of left and right multiplication operators [a5],
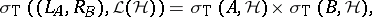 |
and
 |
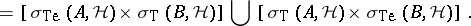 |
During the 1980s and 1990s, Taylor spectral theory has received considerable attention; for further details and information, see [a2], [a11], [a20], [a10], [a1]. There is also a parallel "local spectral theory" , described in [a11], [a12] and [a20].
References
| [a1] | E. Albrecht, F.-H. Vasilescu, "Semi-Fredholm complexes" Oper. Th. Adv. Appl. , 11 (1983) pp. 15–39 MR0789629 Zbl 0527.47008 |
| [a2] | C.-G. Ambrozie, F.-H. Vasilescu, "Banach space complexes" , Kluwer Acad. Publ. (1995) MR1357165 Zbl 0837.47009 |
| [a3] | C. Berger, L. Coburn, A. Koranyi, "Opérateurs de Wiener–Hopf sur les spheres de Lie" C.R. Acad. Sci. Paris Sér. A , 290 (1980) pp. 989–991 MR584284 Zbl 0436.47021 |
| [a4] | C. Berger, L. Coburn, "Wiener–Hopf operators on 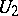 " Integral Eq. Oper. Th. , 2 (1979) pp. 139–173 MR0543881 Zbl 0434.47019 " Integral Eq. Oper. Th. , 2 (1979) pp. 139–173 MR0543881 Zbl 0434.47019 |
| [a5] | R. Curto, L. Fialkow, "The spectral picture of 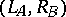 " J. Funct. Anal. , 71 (1987) pp. 371–392 MR0880986 Zbl 0626.47018 " J. Funct. Anal. , 71 (1987) pp. 371–392 MR0880986 Zbl 0626.47018 |
| [a6] | R. Curto, P. Muhly, "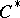 -algebras of multiplication operators on Bergman spaces" J. Funct. Anal. , 64 (1985) pp. 315–329 MR0813203 Zbl 0583.46049 -algebras of multiplication operators on Bergman spaces" J. Funct. Anal. , 64 (1985) pp. 315–329 MR0813203 Zbl 0583.46049 |
| [a7] | R. Curto, N. Salinas, "Spectral properties of cyclic subnormal 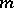 -tuples" Amer. J. Math. , 107 (1985) pp. 113–138 MR778091 -tuples" Amer. J. Math. , 107 (1985) pp. 113–138 MR778091 |
| [a8] | R. Curto, K. Yan, "The spectral picture of Reinhardt measures" J. Funct. Anal. , 131 (1995) pp. 279–301 MR1345033 Zbl 0826.47002 |
| [a9] | R. Curto, "Spectral permanence for joint spectra" Trans. Amer. Math. Soc. , 270 (1982) pp. 659–665 MR0645336 Zbl 0508.47039 Zbl 0491.47020 |
| [a10] | R. Curto, "Applications of several complex variables to multiparameter spectral theory" J.B. Conway (ed.) B.B. Morrel (ed.) , Surveys of Some Recent Results in Operator Theory II , Pitman Res. Notes in Math. , 192 , Longman Sci. Tech. (1988) pp. 25–90 MR0976843 Zbl 0827.47005 |
| [a11] | J. Eschmeier, M. Putinar, "Spectral decompositions and analytic sheaves" , London Math. Soc. Monographs , Oxford Sci. Publ. (1996) MR1420618 Zbl 0855.47013 |
| [a12] | K. Laursen, M. Neumann, "Introduction to local spectral theory" , London Math. Soc. Monographs , Oxford Univ. Press (2000) MR1747914 Zbl 0957.47004 |
| [a13] | M. Putinar, "Uniqueness of Taylor's functional calculus" Proc. Amer. Math. Soc. , 89 (1983) pp. 647–650 MR718990 |
| [a14] | M. Putinar, "Spectral inclusion for subnormal  -tuples" Proc. Amer. Math. Soc. , 90 (1984) pp. 405–406 MR728357 -tuples" Proc. Amer. Math. Soc. , 90 (1984) pp. 405–406 MR728357 |
| [a15] | N. Salinas, A. Sheu, H. Upmeier, "Toeplitz operators on pseudoconvex domains and foliation 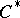 -algebras" Ann. of Math. , 130 (1989) pp. 531–565 MR1025166 -algebras" Ann. of Math. , 130 (1989) pp. 531–565 MR1025166 |
| [a16] | N. Salinas, "The 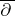 -formalism and the -formalism and the 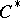 -algebra of the Bergman -algebra of the Bergman  -tuple" J. Oper. Th. , 22 (1989) pp. 325–343 MR1043731 -tuple" J. Oper. Th. , 22 (1989) pp. 325–343 MR1043731 |
| [a17] | J.L. Taylor, "A joint spectrum for several commuting operators" J. Funct. Anal. , 6 (1970) pp. 172–191 MR0268706 Zbl 0233.47024 |
| [a18] | J.L. Taylor, "The analytic functional calculus for several commuting operators" Acta Math. , 125 (1970) pp. 1–48 MR0271741 Zbl 0233.47025 |
| [a19] | H. Upmeier, "Toeplitz 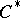 -algebras on bounded symmetric domains" Ann. of Math. , 119 (1984) pp. 549–576 MR744863 -algebras on bounded symmetric domains" Ann. of Math. , 119 (1984) pp. 549–576 MR744863 |
| [a20] | F.-H. Vasilescu, "Analytic functional calculus and spectral decompositions" , Reidel (1982) MR0690957 Zbl 0495.47013 |
| [a21] | U. Venugopalkrishna, "Fredholm operators associated with strongly pseudoconvex domains in 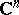 " J. Funct. Anal. , 9 (1972) pp. 349–373 MR0315502 Zbl 0241.47023 " J. Funct. Anal. , 9 (1972) pp. 349–373 MR0315502 Zbl 0241.47023 |
Taylor joint spectrum. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Taylor_joint_spectrum&oldid=14902