Difference between revisions of "Outer measure"
(Importing text file) |
(→References: Royden: internal link) |
||
| Line 30: | Line 30: | ||
====References==== | ====References==== | ||
| − | <table><TR><TD valign="top">[a1]</TD> <TD valign="top"> H.L. Royden, | + | <table><TR><TD valign="top">[a1]</TD> <TD valign="top"> H.L. Royden, [[Royden, "Real analysis"|"Real analysis"]], Macmillan (1968)</TD></TR></table> |
Revision as of 18:06, 26 April 2012
A non-negative set function, denoted by 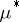 , defined on a countably-additive class of sets that contains in addition to a set itself also any one of its subsets, and having the following properties:
, defined on a countably-additive class of sets that contains in addition to a set itself also any one of its subsets, and having the following properties:
monotony, i.e.
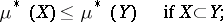 |
countable semi-additivity, i.e.
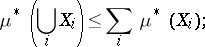 |
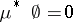 , where
, where 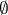 is the empty set.
is the empty set.
An outer measure defined on all subsets of a metric space is said to be an outer measure in the sense of Carathéodory, or a metric outer measure, if
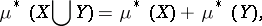 |
provided that 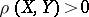 , where
, where 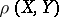 is the distance between the sets
is the distance between the sets 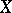 and
and 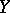 . If an outer measure
. If an outer measure 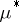 is given, it is possible to specify the class of measurable sets on which
is given, it is possible to specify the class of measurable sets on which 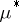 becomes a measure (cf. also Carathéodory measure).
becomes a measure (cf. also Carathéodory measure).
Outer measures result, in particular, from the construction of the extension of a measure from a ring 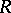 onto the
onto the 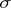 -ring generated by it.
-ring generated by it.
In the classical theory of the Lebesgue measure [1] the outer measure of a set is defined as the greatest lower bound of the measures of the open sets containing the given set; the inner measure of a set is defined as the least upper bound of the measures of the closed sets contained in the given set.
References
| [1] | I.P. Natanson, "Theory of functions of a real variable" , 1–2 , F. Ungar (1955–1961) (Translated from Russian) |
| [2] | S. Saks, "Theory of the integral" , Hafner (1952) (Translated from French) |
| [3] | P.R. Halmos, "Measure theory" , v. Nostrand (1950) |
Comments
References
| [a1] | H.L. Royden, "Real analysis", Macmillan (1968) |
Outer measure. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Outer_measure&oldid=14673