Difference between revisions of "Linear system"
(Importing text file) |
Ulf Rehmann (talk | contribs) m (MR/ZBL numbers added) |
||
| Line 23: | Line 23: | ||
====References==== | ====References==== | ||
| − | <table><TR><TD valign="top">[1]</TD> <TD valign="top"> | + | <table><TR><TD valign="top">[1]</TD> <TD valign="top"> I.R. Shafarevich, "Algebraic surfaces" ''Proc. Steklov Inst. Math.'' , '''75''' (1967) ''Trudy Mat. Inst. Steklov.'' , '''75''' (1965) {{MR|1392959}} {{MR|1060325}} {{ZBL|0830.00008}} {{ZBL|0733.14015}} {{ZBL|0832.14026}} {{ZBL|0509.14036}} {{ZBL|0492.14024}} {{ZBL|0379.14006}} {{ZBL|0253.14006}} {{ZBL|0154.21001}} </TD></TR><TR><TD valign="top">[2]</TD> <TD valign="top"> D. Mumford, "Lectures on curves on an algebraic surface" , Princeton Univ. Press (1966) {{MR|0209285}} {{ZBL|0187.42701}} </TD></TR><TR><TD valign="top">[3]</TD> <TD valign="top"> O. Zariski, "Algebraic surfaces" , Springer (1971) {{MR|0469915}} {{ZBL|0219.14020}} </TD></TR></table> |
| Line 32: | Line 32: | ||
<table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/l/l059/l059470/l05947055.png" /></td> </tr></table> | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/l/l059/l059470/l05947055.png" /></td> </tr></table> | ||
| − | where the <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/l/l059/l059470/l05947056.png" /> define individual curves, surfaces, etc. If the family is one-dimensional (i.e. through a point in general position passes one member of the family), one speaks of a pencil; a two-dimensional family (i.e. two different members of the family pass through a point in general position) is called a net; and a three- (or higher-) dimensional family is called a web, [[#References|[a1]]]. Instead of | + | where the <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/l/l059/l059470/l05947056.png" /> define individual curves, surfaces, etc. If the family is one-dimensional (i.e. through a point in general position passes one member of the family), one speaks of a pencil; a two-dimensional family (i.e. two different members of the family pass through a point in general position) is called a net; and a three- (or higher-) dimensional family is called a web, [[#References|[a1]]]. Instead of "net" the term "bundlebundle" is also occasionally used and instead of "web" one also sometimes finds "net" . |
Quite generally, if <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/l/l059/l059470/l05947057.png" /> is an open subset of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/l/l059/l059470/l05947058.png" />, a codimension <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/l/l059/l059470/l05947061.png" /> <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/l/l059/l059470/l05947062.png" />-web on <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/l/l059/l059470/l05947063.png" /> is defined by <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/l/l059/l059470/l05947064.png" /> foliations of codimension <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/l/l059/l059470/l05947065.png" /> on <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/l/l059/l059470/l05947066.png" /> such that for each <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/l/l059/l059470/l05947067.png" /> the <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/l/l059/l059470/l05947068.png" /> leaves passing through <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/l/l059/l059470/l05947069.png" /> are in general position. Cf. also [[Web|Web]]. Especially in the case of a codimension <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/l/l059/l059470/l05947070.png" /> <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/l/l059/l059470/l05947071.png" />-web, i.e. an <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/l/l059/l059470/l05947073.png" />-web of curves, on <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/l/l059/l059470/l05947074.png" /> (same <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/l/l059/l059470/l05947075.png" />) the word [[Net|net]] is often used. | Quite generally, if <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/l/l059/l059470/l05947057.png" /> is an open subset of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/l/l059/l059470/l05947058.png" />, a codimension <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/l/l059/l059470/l05947061.png" /> <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/l/l059/l059470/l05947062.png" />-web on <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/l/l059/l059470/l05947063.png" /> is defined by <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/l/l059/l059470/l05947064.png" /> foliations of codimension <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/l/l059/l059470/l05947065.png" /> on <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/l/l059/l059470/l05947066.png" /> such that for each <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/l/l059/l059470/l05947067.png" /> the <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/l/l059/l059470/l05947068.png" /> leaves passing through <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/l/l059/l059470/l05947069.png" /> are in general position. Cf. also [[Web|Web]]. Especially in the case of a codimension <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/l/l059/l059470/l05947070.png" /> <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/l/l059/l059470/l05947071.png" />-web, i.e. an <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/l/l059/l059470/l05947073.png" />-web of curves, on <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/l/l059/l059470/l05947074.png" /> (same <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/l/l059/l059470/l05947075.png" />) the word [[Net|net]] is often used. | ||
| − | The phrase | + | The phrase "linear system" of course also occurs (as an abbreviation) in many other parts of mathematics. E.g. in differential equation theory: for system of linear differential equations, and in control and systems theory: for linear input/output systems, linear dynamical systems or linear control system. |
====References==== | ====References==== | ||
| − | <table><TR><TD valign="top">[a1]</TD> <TD valign="top"> | + | <table><TR><TD valign="top">[a1]</TD> <TD valign="top"> J.A. Todd, "Projective and analytical geometry" , Pitman (1947) pp. Chapt. VI {{MR|1527119}} {{MR|0024624}} {{ZBL|0031.06701}} </TD></TR></table> |
Revision as of 16:59, 15 April 2012
A family of effective linearly equivalent divisors (cf. Divisor) on an algebraic variety, parametrized by projective space.
Let 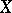 be a non-singular algebraic variety over a field
be a non-singular algebraic variety over a field 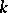 ,
, 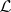 an invertible sheaf on
an invertible sheaf on 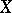 ,
, 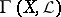 the space of global sections of
the space of global sections of 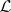 , and
, and 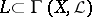 a finite-dimensional subspace. If
a finite-dimensional subspace. If 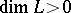 , then the divisors determined by zero sections of
, then the divisors determined by zero sections of  are linearly equivalent and effective. A linear system is the projective space
are linearly equivalent and effective. A linear system is the projective space 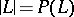 of one-dimensional subspaces of
of one-dimensional subspaces of 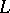 that parametrizes these divisors. If
that parametrizes these divisors. If 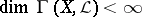 , then the linear system
, then the linear system  is said to be complete; it is denoted by
is said to be complete; it is denoted by 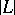 .
.
Let  be a basis of
be a basis of 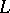 . It defines a rational mapping
. It defines a rational mapping 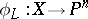 by the formula
by the formula
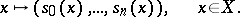 |
One usually says that  is defined by the linear system
is defined by the linear system 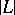 . The image
. The image 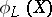 does not lie in any hyperplane of
does not lie in any hyperplane of 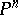 (see [2]). Conversely, every rational mapping
(see [2]). Conversely, every rational mapping 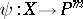 having this property is defined by some linear system.
having this property is defined by some linear system.
A fixed component of a linear system 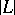 is an effective divisor
is an effective divisor 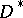 on
on 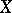 such that
such that 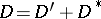 for any
for any 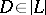 , where
, where 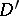 is an effective divisor. When
is an effective divisor. When 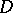 runs through
runs through  , the divisors
, the divisors  form a linear system
form a linear system  of the same dimension as
of the same dimension as 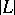 . The mapping
. The mapping 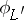 coincides with
coincides with 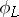 . Therefore, in considering
. Therefore, in considering 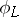 one may assume that
one may assume that 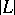 does not have fixed components. In this case
does not have fixed components. In this case 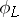 is not defined exactly on the basic set of
is not defined exactly on the basic set of 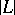 .
.
Examples.
1) Let 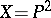 and
and 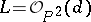 ,
, 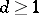 ; then the sections of
; then the sections of 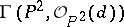 can be identified with forms of degree
can be identified with forms of degree 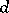 on
on 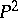 , and the complete linear system
, and the complete linear system 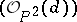 can be identified with the set of all curves of order
can be identified with the set of all curves of order 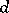 .
.
2) The standard quadratic transformation 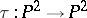 (see Cremona transformation) is defined by the linear system of conics passing through the points
(see Cremona transformation) is defined by the linear system of conics passing through the points 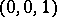 ,
, 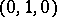 ,
,  .
.
3) The Geiser involution 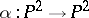 is defined by the linear system of curves of order 8 passing with multiplicity 3 through 7 points in general position (cf. Point in general position).
is defined by the linear system of curves of order 8 passing with multiplicity 3 through 7 points in general position (cf. Point in general position).
4) The Bertini involution 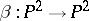 is defined by the linear system of curves of order 17 passing with multiplicity 6 through 8 points in general position.
is defined by the linear system of curves of order 17 passing with multiplicity 6 through 8 points in general position.
References
| [1] | I.R. Shafarevich, "Algebraic surfaces" Proc. Steklov Inst. Math. , 75 (1967) Trudy Mat. Inst. Steklov. , 75 (1965) MR1392959 MR1060325 Zbl 0830.00008 Zbl 0733.14015 Zbl 0832.14026 Zbl 0509.14036 Zbl 0492.14024 Zbl 0379.14006 Zbl 0253.14006 Zbl 0154.21001 |
| [2] | D. Mumford, "Lectures on curves on an algebraic surface" , Princeton Univ. Press (1966) MR0209285 Zbl 0187.42701 |
| [3] | O. Zariski, "Algebraic surfaces" , Springer (1971) MR0469915 Zbl 0219.14020 |
Comments
In classical (elementary) projective and analytic geometry one speaks of linear systems of curves, surfaces, quadrics, etc. These are families of curves, surfaces, etc. of the form
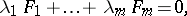 |
where the 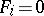 define individual curves, surfaces, etc. If the family is one-dimensional (i.e. through a point in general position passes one member of the family), one speaks of a pencil; a two-dimensional family (i.e. two different members of the family pass through a point in general position) is called a net; and a three- (or higher-) dimensional family is called a web, [a1]. Instead of "net" the term "bundlebundle" is also occasionally used and instead of "web" one also sometimes finds "net" .
define individual curves, surfaces, etc. If the family is one-dimensional (i.e. through a point in general position passes one member of the family), one speaks of a pencil; a two-dimensional family (i.e. two different members of the family pass through a point in general position) is called a net; and a three- (or higher-) dimensional family is called a web, [a1]. Instead of "net" the term "bundlebundle" is also occasionally used and instead of "web" one also sometimes finds "net" .
Quite generally, if 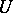 is an open subset of
is an open subset of 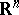 , a codimension
, a codimension 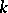
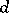 -web on
-web on 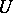 is defined by
is defined by 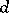 foliations of codimension
foliations of codimension 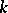 on
on 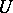 such that for each
such that for each 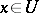 the
the 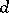 leaves passing through
leaves passing through  are in general position. Cf. also Web. Especially in the case of a codimension
are in general position. Cf. also Web. Especially in the case of a codimension 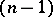
 -web, i.e. an
-web, i.e. an  -web of curves, on
-web of curves, on  (same
(same  ) the word net is often used.
) the word net is often used.
The phrase "linear system" of course also occurs (as an abbreviation) in many other parts of mathematics. E.g. in differential equation theory: for system of linear differential equations, and in control and systems theory: for linear input/output systems, linear dynamical systems or linear control system.
References
| [a1] | J.A. Todd, "Projective and analytical geometry" , Pitman (1947) pp. Chapt. VI MR1527119 MR0024624 Zbl 0031.06701 |
Linear system. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Linear_system&oldid=14380