Difference between revisions of "Ellipsoid"
(Importing text file) |
|||
| Line 1: | Line 1: | ||
''(real)'' | ''(real)'' | ||
| − | A closed central [[Surface of the second order|surface of the second order]] (see Fig.). | + | A closed central [[Surface of the second order|surface of the second order]] (see Fig.). |
<img style="border:1px solid;" src="https://www.encyclopediaofmath.org/legacyimages/common_img/e035410a.gif" /> | <img style="border:1px solid;" src="https://www.encyclopediaofmath.org/legacyimages/common_img/e035410a.gif" /> | ||
| Line 8: | Line 8: | ||
The canonical equation of an ellipsoid has the form | The canonical equation of an ellipsoid has the form | ||
| + | $$ | ||
| + | \frac{x^2}{a^2} + \frac{y^2}{b^2} + \frac{z^2}{c^2} = 1 | ||
| + | $$ | ||
| + | The positive numbers $a$, $b$ and $c$ and the segments of corresponding lengths are called the semi-axes of the ellipsoid. The section of an ellipsoid by any plane is an ellipse. | ||
| − | + | If two semi-axes of an ellipsoid are equal, the ellipsoid is called an ellipsoid of revolution, and the sections of an ellipsoid of revolution by planes parallel to the plane of the equal semi-axes are circles. When $a=b=c$, the ellipsoid is a sphere. The centre of symmetry of an ellipsoid is called the centre of the ellipsoid. | |
| − | |||
| − | |||
| − | |||
| − | If two semi-axes of an ellipsoid are equal, the ellipsoid is called an ellipsoid of revolution, and the sections of an ellipsoid of revolution by planes parallel to the plane of the equal semi-axes are circles. When | ||
A second-order surface with canonical equation | A second-order surface with canonical equation | ||
| − | + | $$ | |
| − | + | \frac{x^2}{a^2} + \frac{y^2}{b^2} + \frac{z^2}{c^2} = 1 | |
| − | + | $$ | |
is called an imaginary ellipsoid. | is called an imaginary ellipsoid. | ||
| + | ====Comments==== | ||
| − | |||
| − | |||
As the name suggests, an imaginary ellipsoid does not have real points. | As the name suggests, an imaginary ellipsoid does not have real points. | ||
| − | Other characterizations of an ellipsoid are as follows | + | Other characterizations of an ellipsoid are as follows: An ellipsoid is the affine image of a [[Sphere|sphere]]; an ellipsoid is a non-degenerate [[Quadric|quadric]] without real points at infinity. |
| − | |||
| − | An ellipsoid is the affine image of a [[Sphere|sphere]]; an ellipsoid is a non-degenerate [[Quadric|quadric]] without real points at infinity. | ||
A systematic treatment of ellipsoids is given in [[#References|[a1]]], Chapt. 15 and [[#References|[a2]]]. A more advanced survey is contained in [[#References|[a3]]]. | A systematic treatment of ellipsoids is given in [[#References|[a1]]], Chapt. 15 and [[#References|[a2]]]. A more advanced survey is contained in [[#References|[a3]]]. | ||
| − | ====References==== | + | ====References==== |
| − | <table><TR><TD valign="top">[a1]</TD> <TD valign="top"> | + | <table><TR><TD valign="top">[a1]</TD> <TD valign="top"> M. Berger, "Geometry" , '''II''' , Springer (1987)</TD></TR><TR><TD valign="top">[a2]</TD> <TD valign="top"> J. Coolidge, "A history of the conic sections and quadric surfaces" , Dover, reprint (1968)</TD></TR><TR><TD valign="top">[a3]</TD> <TD valign="top"> C.M. Petty, "Ellipsoids" P.M. Gruber (ed.) J.M. Wills (ed.) , ''Convexity and its applications'' , Birkhäuser (1983) pp. 264–276</TD></TR></table> |
Revision as of 10:30, 24 April 2012
(real)
A closed central surface of the second order (see Fig.).
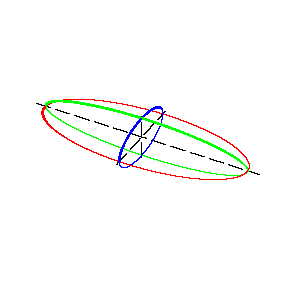
Figure: e035410a
The canonical equation of an ellipsoid has the form $$ \frac{x^2}{a^2} + \frac{y^2}{b^2} + \frac{z^2}{c^2} = 1 $$ The positive numbers $a$, $b$ and $c$ and the segments of corresponding lengths are called the semi-axes of the ellipsoid. The section of an ellipsoid by any plane is an ellipse.
If two semi-axes of an ellipsoid are equal, the ellipsoid is called an ellipsoid of revolution, and the sections of an ellipsoid of revolution by planes parallel to the plane of the equal semi-axes are circles. When $a=b=c$, the ellipsoid is a sphere. The centre of symmetry of an ellipsoid is called the centre of the ellipsoid.
A second-order surface with canonical equation $$ \frac{x^2}{a^2} + \frac{y^2}{b^2} + \frac{z^2}{c^2} = 1 $$ is called an imaginary ellipsoid.
Comments
As the name suggests, an imaginary ellipsoid does not have real points.
Other characterizations of an ellipsoid are as follows: An ellipsoid is the affine image of a sphere; an ellipsoid is a non-degenerate quadric without real points at infinity.
A systematic treatment of ellipsoids is given in [a1], Chapt. 15 and [a2]. A more advanced survey is contained in [a3].
References
| [a1] | M. Berger, "Geometry" , II , Springer (1987) |
| [a2] | J. Coolidge, "A history of the conic sections and quadric surfaces" , Dover, reprint (1968) |
| [a3] | C.M. Petty, "Ellipsoids" P.M. Gruber (ed.) J.M. Wills (ed.) , Convexity and its applications , Birkhäuser (1983) pp. 264–276 |
Ellipsoid. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Ellipsoid&oldid=14258